

分析 (1)由C有12人,占24%,即可求得该班的总人数,继而求得A与E的人数,即可补全频数分布直方图;
(2)由(1)可得“足球”在扇形的圆心角是360°×$\frac{7}{50}$;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与选出的2人恰好1人选修篮球,1人选修足球的情况,再利用概率公式即可求得答案.
解答 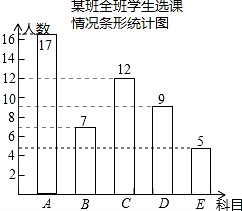 解:(1)∵C有12人,占24%,
解:(1)∵C有12人,占24%,
∴该班的总人数有:12÷24%=50(人),
∴E有:50×10%=5(人),
A有50-7-12-9-5=17(人),
补全频数分布直方图为:
(2)“足球”在扇形的圆心角是:360°×$\frac{7}{50}$=50.4°;
(3)画树状图得: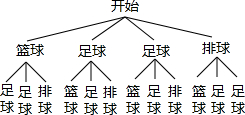
∵共有12种等可能的结果,选出的2人恰好1人选修篮球,1人选修足球的有4种情况,
∴选出的2人恰好1人选修篮球,1人选修足球的概率为:$\frac{4}{12}$=$\frac{1}{3}$.
点评 此题考查的是用列表法或树状图法求概率以及扇形统计图与频数分布直方图的知识.用到的知识点为:概率=所求情况数与总情况数之比.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线a∥b,直线c交a、b于点A、B.
已知直线a∥b,直线c交a、b于点A、B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,AB是⊙O上的直径,弦CD⊥AB于点G,点F是CD上的一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②GF=2;③tan∠E=$\frac{\sqrt{5}}{2}$;④S△ADE=7$\sqrt{5}$.其中正确的是①②④(写出所有正确结论的序号)
如图,AB是⊙O上的直径,弦CD⊥AB于点G,点F是CD上的一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3,给出下列结论:①△ADF∽△AED;②GF=2;③tan∠E=$\frac{\sqrt{5}}{2}$;④S△ADE=7$\sqrt{5}$.其中正确的是①②④(写出所有正确结论的序号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,D,E分别在等边三角形ABC中边CB和边BC的延长线上.
如图,D,E分别在等边三角形ABC中边CB和边BC的延长线上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将一枚硬币放到数轴上,把与数轴的原点重合的点记作点A,数轴上的单位长度等于硬币的直径.将硬币沿数轴的正方向滚动以周,点A到达数轴上的点A′处,点A′对应的实数是π.
如图,将一枚硬币放到数轴上,把与数轴的原点重合的点记作点A,数轴上的单位长度等于硬币的直径.将硬币沿数轴的正方向滚动以周,点A到达数轴上的点A′处,点A′对应的实数是π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 函数的图象不经过原点 | B. | 函数的图象一定在一、三象限 | ||
| C. | y的值随x值的增大而减小 | D. | 点($\frac{5}{2}$,2)在函数的图象上 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com