
分析 利用配方法把一般式化为顶点式即可.
解答 解:y=x2-2x+3=(x-1)2+2.
故答案为y=(x-1)2+2.
点评 本题考查了二次函数的三种形式:一般式:y=ax2+bx+c(a,b,c是常数,a≠0),该形式的优势是能直接根据解析式知道抛物线与y轴的交点坐标是(0,c);顶点式:y=a(x-h)2+k(a,h,k是常数,a≠0),其中(h,k)为顶点坐标,该形式的优势是能直接根据解析式得到抛物线的顶点坐标为(h,k);交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0),该形式的优势是能直接根据解析式得到抛物线与x轴的两个交点坐标(x1,0),(x2,0).


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案科目:初中数学 来源: 题型:选择题
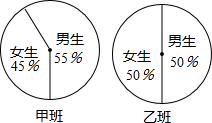
| A. | 甲班男生比乙班男生多 | B. | 乙班女生比甲班女生多 | ||
| C. | 乙班女生与乙班男生一样多 | D. | 甲、乙两班人数一样多 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
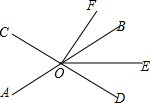 如图,直线AB、CD相交于点O,OE平分∠BOD.
如图,直线AB、CD相交于点O,OE平分∠BOD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知△ABC是等腰直角三角形,∠ACB=90°,P为斜边AB上一点,PF⊥BC于点F,PE⊥AC于点E.若S△APE=7,S△PBF=2,则PC的长为( )
如图,已知△ABC是等腰直角三角形,∠ACB=90°,P为斜边AB上一点,PF⊥BC于点F,PE⊥AC于点E.若S△APE=7,S△PBF=2,则PC的长为( )| A. | 5 | B. | 3$\sqrt{2}$ | C. | $\sqrt{53}$ | D. | 3$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
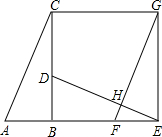 如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.
如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.查看答案和解析>>
科目:初中数学 来源:2016-2017学年河南省七年级下学期第一次月考(3月)数学试卷(解析版) 题型:判断题
如图,已知AB∥CD,∠B=65°,CM平分∠BCE,∠MCN=90°,求∠DCN的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com