考点:二次函数与不等式(组),待定系数法求一次函数解析式,待定系数法求二次函数解析式
专题:
分析:(1)将已知两点坐标代入直线与抛物线解析式求出各字母的值,即可确定出各自的解析式;
(2)观察图象,直线y1落在抛物线y2上方的部分对应的x的取值即为所求x的取值范围;
(3)设C的坐标为(x,-x2+3.5x+2),根据S△ABC=S△AOC+S△BOC-S△AOB=6列出方程,解方程即可.
解答:解:(1)将(4,0)与(0,2)分别代入直线解析式得:
,
解得:
,
即直线解析式为y
1=-
x+2;
将(4,0)与(0,2)分别代入抛物线解析式得:
,
解得:
,
即抛物线解析式为y
2=-x
2+3.5x+2;
(2)根据两函数交点坐标为(0,2),(4,0),
由图象得:当y
1>y
2时,x的取值范围为x<0或x>4;
(3)设C的坐标为(x,-x
2+3.5x+2),则0<x<4.
∵S
△ABC=6,
∴S
△AOC+S
△BOC-S
△AOB=6,
∴
×4×(-x
2+3.5x+2)+
×2x-
×4×2=6,
整理得x
2-4x+3=0,
解得x
1=1,x
2=3,
当x
1=1时,-x
2+3.5x+2=-1+3.5+2=4.5;
当x
2=3时,-x
2+3.5x+2=-9+10.5+2=3.5;
∴C的坐标为(1,4.5)或(3,3.5).
点评:此题考查了二次函数与不等式,利用待定系数法求一次函数、二次函数解析式,三角形的面积,熟练掌握待定系数法是解本题的关键.

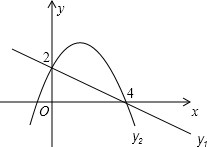 如图,已知直线y1=kx+n与抛物线y2=-x2+bx+c都经过A(4,0)和B(0,2).
如图,已知直线y1=kx+n与抛物线y2=-x2+bx+c都经过A(4,0)和B(0,2).

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案