
ЁОЬтФПЁПЃЈ10ЗжЃЉШчЭМЃЌвЛаЁЧђДгаБЦТOЕуДІХзГіЃЌЧђЕФХзГіТЗЯпПЩвдгУЖўДЮКЏЪ§y=Љx2+4xПЬЛЃЌаБЦТПЩвдгУвЛДЮКЏЪ§y=![]() xПЬЛЃЎ
xПЬЛЃЎ
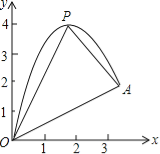
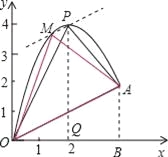
ЃЈ1ЃЉЧыгУХфЗНЗЈЧѓЖўДЮКЏЪ§ЭМЯѓЕФзюИпЕуPЕФзјБъЃЛ
ЃЈ2ЃЉаЁЧђЕФТфЕуЪЧAЃЌЧѓЕуAЕФзјБъЃЛ
ЃЈ3ЃЉСЌНгХзЮяЯпЕФзюИпЕуPгыЕуOЁЂAЕУЁїPOAЃЌЧѓЁїPOAЕФУцЛ§ЃЛ
ЃЈ4ЃЉдкOAЩЯЗНЕФХзЮяЯпЩЯДцдквЛЕуMЃЈMгыPВЛжиКЯЃЉЃЌЁїMOAЕФУцЛ§ЕШгкЁїPOAЕФУцЛ§ЃЎЧыжБНгаДГіЕуMЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈ2ЃЌ4ЃЉЃЛЃЈ2ЃЉЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛЃЈ3ЃЉ
ЃЉЃЛЃЈ3ЃЉ![]() ЃЛЃЈ4ЃЉЃЈ
ЃЛЃЈ4ЃЉЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉРћгУХфЗНЗЈХзЮяЯпЕФвЛАуЪНЛЏЮЊЖЅЕуЪНЃЌМДПЩЧѓГіЖўДЮКЏЪ§ЭМЯѓЕФзюИпЕуPЕФзјБъЃЛ
ЃЈ2ЃЉСЊСЂСННтЮіЪНЃЌПЩЧѓГіНЛЕуAЕФзјБъЃЛ
ЃЈ3ЃЉзїPQЁЭxжсгкЕуQЃЌABЁЭxжсгкЕуBЃЎИљОнSЁїPOA=SЁїPOQ+SЁїЬнаЮPQBAЉSЁїBOAЃЌДњШыЪ§жЕМЦЫуМДПЩЧѓНтЃЛ
ЃЈ4ЃЉЙ§PзїOAЕФЦНааЯпЃЌНЛХзЮяЯпгкЕуMЃЌСЌНсOMЁЂAMЃЌгЩгкСНЦНааЯпжЎМфЕФОрРыЯрЕШЃЌИљОнЭЌЕзЕШИпЕФСНИіШ§НЧаЮУцЛ§ЯрЕШЃЌПЩЕУЁїMOAЕФУцЛ§ЕШгкЁїPOAЕФУцЛ§ЃЎЩшжБЯпPMЕФНтЮіЪНЮЊy=![]() x+bЃЌНЋPЃЈ2ЃЌ4ЃЉДњШыЃЌЧѓГіжБЯпPMЕФНтЮіЪНЮЊy=
x+bЃЌНЋPЃЈ2ЃЌ4ЃЉДњШыЃЌЧѓГіжБЯпPMЕФНтЮіЪНЮЊy=![]() x+3ЃЎдйгыХзЮяЯпЕФНтЮіЪНСЊСЂЃЌЕУЕНЗНГЬзщ
x+3ЃЎдйгыХзЮяЯпЕФНтЮіЪНСЊСЂЃЌЕУЕНЗНГЬзщ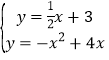 ЃЌНтЗНГЬзщМДПЩЧѓГіЕуMЕФзјБъЃЎ
ЃЌНтЗНГЬзщМДПЩЧѓГіЕуMЕФзјБъЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгЩЬтвтЕУЃЌy=Љx2+4x=ЉЃЈxЉ2ЃЉ2+4ЃЌ
ЙЪЖўДЮКЏЪ§ЭМЯѓЕФзюИпЕуPЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЛ
ЃЈ2ЃЉСЊСЂСННтЮіЪНПЩЕУЃК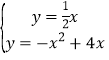 ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌЛђ
ЃЌЛђ![]() ЃЎ
ЃЎ
ЙЪПЩЕУЕуAЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉШчЭМЃЌзїPQЁЭxжсгкЕуQЃЌABЁЭxжсгкЕуBЃЎ
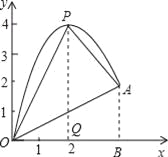
SЁїPOA=SЁїPOQ+SЁїЬнаЮPQBAЉSЁїBOA
=![]() ЁС2ЁС4+
ЁС2ЁС4+![]() ЁСЃЈ
ЁСЃЈ![]() +4ЃЉЁСЃЈ
+4ЃЉЁСЃЈ![]() Љ2ЃЉЉ
Љ2ЃЉЉ![]() ЁС
ЁС![]() ЁС
ЁС![]()
=4+![]() Љ
Љ![]()
=![]() ЃЛ
ЃЛ
ЃЈ4ЃЉЙ§PзїOAЕФЦНааЯпЃЌНЛХзЮяЯпгкЕуMЃЌСЌНсOMЁЂAMЃЌдђЁїMOAЕФУцЛ§ЕШгкЁїPOAЕФУцЛ§ЃЎ
ЩшжБЯпPMЕФНтЮіЪНЮЊy=![]() x+bЃЌ
x+bЃЌ
ЁпPЕФзјБъЮЊЃЈ2ЃЌ4ЃЉЃЌ
Ёр4=![]() ЁС2+bЃЌНтЕУb=3ЃЌ
ЁС2+bЃЌНтЕУb=3ЃЌ
ЁржБЯпPMЕФНтЮіЪНЮЊy=![]() x+3ЃЎ
x+3ЃЎ
гЩ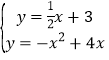 ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ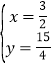 ЃЌ
ЃЌ
ЁрЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЮвУЧЖЈвхЕуP(a ЃЌb )ЕФЁААщЫцЕуЁБЮЊQЃЌЧвЙцЖЈЃКЕБa Ён bЪБЃЌQЮЊ( bЃЌЃa )ЃЛЕБ aЃМb ЪБЃЌQЮЊ( aЃЌЃb)ЃЎ
ЃЈ1ЃЉЕу(2ЃЌ1)ЕФАщЫцЕузјБъЮЊ__________ЃЛ
ЃЈ2ЃЉШєЕуA(a ЃЌ2)ЕФАщЫцЕудкКЏЪ§y=![]() ЕФЭМЯёЩЯЃЌЧѓaЕФжЕЃЛ
ЕФЭМЯёЩЯЃЌЧѓaЕФжЕЃЛ
ЃЈ3ЃЉвбжЊжБЯпlгызјБъжсНЛгк(6ЃЌ0)ЃЌ(0ЃЌ3)СНЕуЃЎНЋжБЯпlЩЯЫљгаЕуЕФАщЫцЕузщГЩвЛИіаТЕФЭМаЮМЧзїMЃЎЧыжБНгаДГіжБЯпy=ЁЊx+cгыЭМаЮMгаНЛЕуЪБЯргІЕФcЕФШЁжЕЗЖЮЇЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзввСНИіЙЄГЬЖгГаАќСЫЕиЬњФГБъЖЮШЋГЄ3900УзЕФЪЉЙЄШЮЮёЃЌЗжБ№ДгФЯЃЌББСНИіЗНЯђЭЌЪБЯђЧАОђНјЁЃвбжЊМзЙЄГЬЖгБШввЙЄГЬЖгЦНОљУПЬьЖрОђНј0.4УзОЙ§13ЬьЕФЪЉЙЄСНИіЙЄГЬЖгЙВОђНјСЫ156Уз.
(1)ЧѓМзЃЌввСНИіЙЄГЬЖгЦНОљУПЬьИїОђНјЖрЩйУзЃП
(2)ЮЊМгПьЙЄГЬНјЖШСНЙЄГЬЖгЖМИФНјСЫЪЉЙЄММЪѕЃЌдкЪЃгрЕФЙЄГЬжаЃЌМзЙЄГЬЖгЦНОљУПЬьФмБШдРДЖрОђНј0.4УзЃЌввЙЄГЬЖгЦНОљУПЬьФмБШдРДЖрОђНј0.6УзЃЌАДДЫЪЉЙЄНјЖШФмЙЛБШдРДЩйгУЖрЩйЬьЭъГЩШЮЮёФиЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(7Зж)ШчЭМЃЌвбжЊХзЮяЯпyЃНx2ЃЋbxЃЋcОЙ§A(Ѓ1ЃЌ0)ЃЌB(3ЃЌ0)СНЕуЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪНКЭЖЅЕузјБъЃЛ
(2)ЕБ0ЃМxЃМ3ЪБЃЌЧѓyЕФШЁжЕЗЖЮЇЃЛ
(3)ЕуPЮЊХзЮяЯпЩЯвЛЕуЃЌШєSЁїPABЃН10ЃЌЧѓГіДЫЪБЕуPЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаЫуЪНЃК21ЃН2ЁЂ22ЃН4ЁЂ23ЃН8ЁЂ24ЃН16ЁЂ25ЃН32ЁЂ26ЃН64ЁЂ27ЃН128ЁЂ28ЃН256ЁЃЌгУФуЫљЗЂЯжЕФЙцТЩаДГі21+22+23+24+25+Ё+22018ЕФФЉЮЛЪ§зжЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛСОЛѕГЕДгЛѕГЁ![]() ГіЗЂЃЌЯђЖЋзп2ЧЇУзЕНДяХњЗЂВП
ГіЗЂЃЌЯђЖЋзп2ЧЇУзЕНДяХњЗЂВП![]() ЃЌМЬајЯђЖЋзп1.5ЧЇУзЕНДяЩЬГЁ
ЃЌМЬајЯђЖЋзп1.5ЧЇУзЕНДяЩЬГЁ![]() ЃЌгжЯђЮїзп5.5ЧЇУзЕНДяГЌЪа
ЃЌгжЯђЮїзп5.5ЧЇУзЕНДяГЌЪа![]() ЃЌзюКѓЛиЕНЛѕГЁЃЎ
ЃЌзюКѓЛиЕНЛѕГЁЃЎ
ЃЈ1ЃЉвдЛѕГЁЮЊдЕуЃЌвдЖЋЮЊе§ЗНЯђЃЌгУвЛИіЕЅЮЛГЄЖШБэЪО1ЧЇУзЃЌФуФмдкЪ§жсЩЯЗжБ№БэЪОГіЛѕГЁ![]() ЃЌХњЗЂВП
ЃЌХњЗЂВП![]() ЃЌЩЬГЁ
ЃЌЩЬГЁ![]() ЃЌГЌЪа
ЃЌГЌЪа![]() ЕФЮЛжУТ№ЃП
ЕФЮЛжУТ№ЃП
ЃЈ2ЃЉГЌЪа![]() ОрРыЛѕГЁ
ОрРыЛѕГЁ![]() ЖрдЖЃП
ЖрдЖЃП
ЃЈ3ЃЉДЫЛѕГЕУПЧЇУзКФгЭ0.1Щ§ЃЌУПЩ§ЦћгЭ6.20дЊЃЌЧыМЦЫуДЫЛѕГЕвЛЙВашвЊЖрЩйЦћгЭЗбЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСадЫЫуМАХаЖЯе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. Љ5ЁС![]() ЁТЃЈЉ
ЁТЃЈЉ![]() ЃЉЁС5=1
ЃЉЁС5=1
B. ЗНГЬЃЈx2+xЉ1ЃЉx+3=1гаЫФИіећЪ§Нт
C. ШєaЁС5673=103ЃЌaЁТ103=bЃЌдђaЁСb=![]()
D. гаађЪ§ЖдЃЈm2+1ЃЌmЃЉдкЦНУцжБНЧзјБъЯЕжаЖдгІЕФЕувЛЖЈдкЕквЛЯѓЯо
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
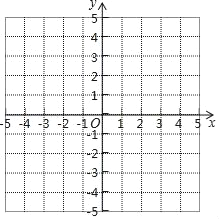
ЁОЬтФПЁПШчЭМЫљЪОЕФзјБъЯЕжаЃЌЁїABCЕФШ§ИіЖЅЕуЕФзјБъвРДЮЮЊAЃЈЉ1ЃЌ2ЃЉЃЌBЃЈЉ4ЃЌ1ЃЉЃЌCЃЈЉ2ЃЌЉ2ЃЉЃЎ
ЃЈ1ЃЉЧыдкетИізјБъЯЕжазїГіЁїABCЙигкyжсЖдГЦЕФЁїA1B1C1ЃЎ
ЃЈ2ЃЉЗжБ№аДГіЕуA1ЁЂB1ЁЂC1ЕФзјБъЃЎ
ЃЈ3ЃЉЧѓЁїA1B1C1ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдкЁїABCКЭЁїDECжаЃЌAC=BCЃЌDC=ECЃЌЁЯACB=ЁЯECD=90ЁуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуAЁЂCЁЂDдкЭЌвЛЬѕжБЯпЩЯЪБЃЌAEгыBDЕФЪ§СПЙиЯЕЪЧ ЃЛ
ЮЛжУЙиЯЕЪЧ ЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуAЁЂCЁЂDВЛдкЭЌвЛЬѕжБЯпЩЯЪБЃЌ(1)жаЕФНсТлЛЙГЩСЂТ№ЃПЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com