
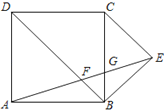
【题目】如图,四边形ABCD是正方形,以BC为底边向正方形外部作等腰直角三角形BCE,连接AE,分别交BD,BC于点F,G,则下列结论:①△AFB∽△ABE;②△ADF∽△GCE;③CG=3BG;④AF=EF,其中正确的有( ).
A.①③B.②④C.①②D.③④
【答案】B
【解析】
连接AC,交BD于O,过点E作EH⊥BC于H,由正方形的性质及等腰直角三角形的性质可得∠ADF=∠ABD=∠BCE=∠CBE=45°,可得∠ABE=135°,根据外角性质可得∠AFD=∠FAB+∠ABF>45°,利用平角定义可得∠AFB<135°,即可证明∠AFB≠∠ABE,可对①进行判断;由EH⊥BC可证明EH//AB,根据平行线的性质可得∠HEG=∠FAB,根据角的和差关系可证明∠DAF=∠CEG,即可证明△ADF∽△GCE;可对②进行判断,由EH//AB可得△HEG∽△BAG,根据相似三角形的性质即可得出BG=2HG,根据等腰直角三角形性质可得CH=BH,进而可得CG=2BG,可对③进行判断;根据正方形的性质可得OA=BE,∠AOF=∠FBE=90°,利用AAS可证明△AOF≌△EBF,可得AF=EF,可对④进行判断;综上即可得答案.
如图,连接AC,交BD于O,过点E作EH⊥BC于H,
∵ABCD是正方形,△BCE是等腰直角三角形,
∴∠ADF=∠ABD=∠BCE=∠CBE=45°,
∴∠ABE=135°,
∵∠AFD=∠BAF+∠ABF=∠BAF+45°>45°,
∴∠AFB=180°-∠AFD<135°,
∴∠AFB≠∠ABE,
∴△AFB与△ABE不相似,故①错误,
∵EH⊥BC,∠ABC=90°,
∴EH//AB,
∴∠HEG=∠FAB,
∴∠AFD=∠FAB+∠ABD=45°+∠HEG=∠CEG,
又∵∠ADB=∠GCE=45°,
∴△ADF∽△GCE,故②正确,
∵EH//AB,
∴△HEG∽△BAG,
∴![]() ,
,
∵△BCE是等腰直角三角形,
∴EH=CH=BH=![]() BC=
BC=![]() AB,
AB,
∴![]() =
=![]() ,即BG=2HG,
,即BG=2HG,
∴CH=BH=3HG,
∴CG=CH+HG=4HG,
∴CG=2BG,故③错误,
∵ABCD是正方形,△BCE是等腰直角三角形,
∴∠AOF=90°,∠FBE=∠DBC+∠CBE=45°+45°=90°,OA=![]() AB,BE=
AB,BE=![]() BC,
BC,
∴∠AOF=∠FBE,OA=BE,
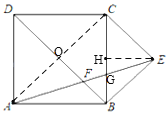
在△AOF和△EBF中,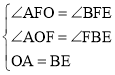 ,
,
∴△AOF≌△EBF,
∴AF=EF,故④正确,
综上所述:正确的结论有②④,
故选:B.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
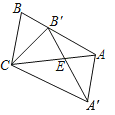
【题目】如图,等腰△ABC的顶角∠A=36°,若将其绕点C顺时针旋转36°,得到△A′B′C,点B′在AB边上,A′B′交AC于E,连接AA′.有下列结论:①△ABC≌△A′B′C;②四边形A′ABC是平行四边形;③图中所有的三角形都是等腰三角形;其中正确的结论是( )
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中有点A(1,5),B(2,2),将线段AB绕P点逆时针旋转90°得到线段CD,A和C对应,B和D对应.
(1)若P为AB中点,画出线段CD,保留作图痕迹;
(2)若D(6,2),则P点的坐标为 ,C点坐标为 .
(3)若C为直线![]() 上的动点,则P点横、纵坐标之间的关系为 .
上的动点,则P点横、纵坐标之间的关系为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为![]() 个单位的正方形,在建立平面直角坐标系后,
个单位的正方形,在建立平面直角坐标系后,![]() 的顶点均在格点上,点
的顶点均在格点上,点![]() 的坐标为
的坐标为![]() .
.
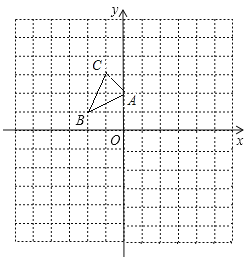
![]() 以点
以点![]() 为位似中心,在
为位似中心,在![]() 轴的左侧将
轴的左侧将![]() 放大得到
放大得到![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的
面积的![]() 倍,在网格中画出图形,并直接写出点
倍,在网格中画出图形,并直接写出点![]() 所对应的点
所对应的点![]() 的坐标.
的坐标.
![]() 在网格中,画出
在网格中,画出![]() 绕原点
绕原点![]() 顺时针旋转
顺时针旋转![]() 的
的![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春节期间,支付宝“集五福”活动中的“集五福”福卡共分为5种,分别为富强福、和谐福、友善福、爱国福、敬业福,从国家、社会和个人三个层面体现了社会主义核心价值观的价值目标.
(1)小明一家人春节期间参与了支付宝“集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给他们其中一个人,两个人各设计了一个游戏,获胜者得到“敬业福”.
在一个不透明盒子里放入标号分别为1,2,3,4的四个小球,这些小球除了标号数字外都相同,将小球摇匀.
小明的游戏规则是:从盒子中随机摸出一个小球,摸到标号数字为奇数小球,则判小明获胜,否则,判姐姐获胜.请判断,此游戏规则对小明和姐姐公平吗?说明理由.
姐姐的游戏规则是:小明从盒子中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,姐姐再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判小明获胜,若两次摸到小球的标号数字为一奇一偶,则判姐姐获胜.请用列表法或画树状图的方法进行判断此游戏规则对小明和姐姐是否公平.
(2)“五福”中体现了社会主义核心价值观的价值目标的个人层面有哪些?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.
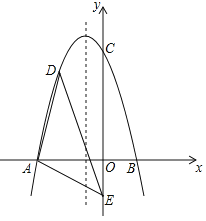
(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示平面直角坐标系中,点A,C分别在x轴和y轴上,点B在第一象限,BC=BA,∠ABC=90°,反比例函数y=![]() .(x>0)的图象经过点B,若OB=2
.(x>0)的图象经过点B,若OB=2![]() ,则k的值为_____.
,则k的值为_____.
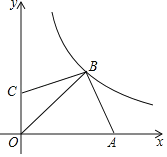
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光污染是继废气、废水、废渣和噪声等污染之后的一种新的环境污染源,主要包括白亮污染、人工白昼污染和彩光污染,如图,小明家正对面的高楼外墙上安装着一幅巨型广告宣传牌AB,小明想要测量窗外的广告宣传牌AB的高度,他发现晚上家里熄灯后对面楼上的广告宣传牌从A处发出的光恰好从窗户的最高点C处射进房间落在地板上F处,从窗户的最低点D处射进房间向落在地板上E处(B、O、E、F在同一直线E),小明测得窗户距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=3m.请根据以上测量数据,求广告宣传牌AB的高度.
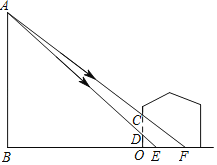
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com