
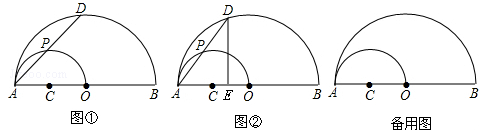
 ;(3)
;(3)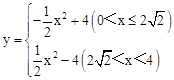 .
. .
.
 时),如图②,连接OP,则∠APO=∠AED.
时),如图②,连接OP,则∠APO=∠AED.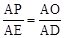 .
.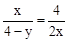 .∴
.∴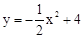 (0<x≤
(0<x≤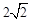 ).
).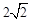 <x<4)时,如图③,
<x<4)时,如图③,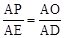 .
. .∴
.∴ (
(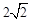 <x<4).
<x<4).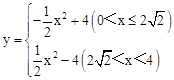 .
.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源:不详 题型:解答题
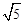 为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数
为半径作圆,与x轴交于A、B两点,与y轴交于C、D两点,二次函数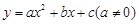 的图象经过点A、B、C,顶点为E.
的图象经过点A、B、C,顶点为E.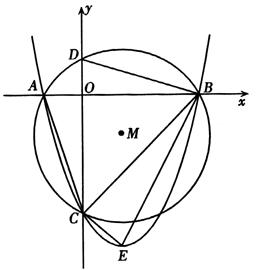
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

 cm/s速度沿AC向点C运动,同时点M从点C出发,以1cm/s的速度沿CD向点D运动,运动时间为t(t>0),连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.判断命题“当点F是边AB中点时,则点M是边CD的三等分点”的真假,并说明理由. (4分)
cm/s速度沿AC向点C运动,同时点M从点C出发,以1cm/s的速度沿CD向点D运动,运动时间为t(t>0),连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.判断命题“当点F是边AB中点时,则点M是边CD的三等分点”的真假,并说明理由. (4分)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 时,
时,  的值为 ;当
的值为 ;当 时,
时, 为 .(用含n的式子表示)
为 .(用含n的式子表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com