
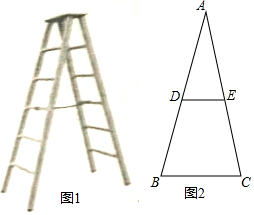
 如图1所示的是由梯子AB和梯子AC搭成的“人字梯”,它的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,将其抽象成图2,其中AB=AC=2米.
如图1所示的是由梯子AB和梯子AC搭成的“人字梯”,它的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,将其抽象成图2,其中AB=AC=2米.分析 (1)直接根据三角形中位线定理即可得出结论;
(2)过点A作AF⊥BC于点F,由锐角三角函数的定义求出BF及AF的长,再根据等腰三角形的性质得出BC的长,进而可得出结论.
解答 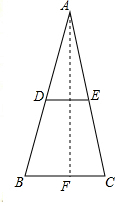 解:(1)∵的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,
解:(1)∵的5个踩档把梯子等分成6份,梯子的第三踩档处有一条绑绳DE,
∴DE是△ABC的中位线,
∴BC=2DE=120(厘米).
答:两梯角之间的距离BC的长是120厘米;
(2)如图,过点A作AF⊥BC于点F,
∵AB=2米,∠ABC=70°,
∴AF=AB•sin70°≈2×0.9397=1.8794(米),BF=AB•cos70°≈2×0.3420=0.684,
∵AB=AC,
∴BC=2BF=1.368(米),
∵DE是△ABC的中位线,
∴DE=$\frac{1}{2}$BC=0.684米.
∵在D,E处打结各需要0.3米的绳子,
∴绳子长=0.3+0.3+0.684=1.284米.
答:他需要的绑绳的长度为1.284米,此时梯子的顶端A离地面BC的高度为1.8794米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,熟记锐角三角函数的定义是解答此题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
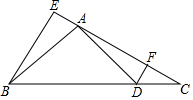 如图,在△ABC中,AB=AC,过A作AD⊥AB交BC于点D,过B作BE⊥AC,交CA延长线于点E,过D作DF⊥AC,垂足为F.若EF=3$\sqrt{3}$.BC=6$\sqrt{2}$.则tan∠C=$\frac{\sqrt{2}}{2}$.
如图,在△ABC中,AB=AC,过A作AD⊥AB交BC于点D,过B作BE⊥AC,交CA延长线于点E,过D作DF⊥AC,垂足为F.若EF=3$\sqrt{3}$.BC=6$\sqrt{2}$.则tan∠C=$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:| 组别 | 成绩(分) | 频数 |
| A | 50≤x<60 | 6 |
| B | 60≤x<70 | m |
| C | 70≤x<80 | 20 |
| D | 80≤x<90 | 36 |
| E | 90≤x<100 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
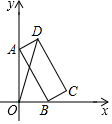 如图,矩形ABCD中,AB=8,BC=3,顶点A,B分别在y轴和x轴上,当点A在y轴上移动时,点B也随之在x轴上移动,在移动过程中,OD的最大值为( )
如图,矩形ABCD中,AB=8,BC=3,顶点A,B分别在y轴和x轴上,当点A在y轴上移动时,点B也随之在x轴上移动,在移动过程中,OD的最大值为( )| A. | 8 | B. | $\sqrt{73}$ | C. | $\sqrt{85}$ | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com