
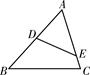
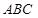 中,
中,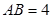 ,当直角三角板
,当直角三角板 的
的 角的顶点
角的顶点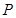 在
在 上移动时,斜边
上移动时,斜边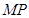 始终经过
始终经过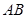 边的中点
边的中点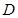 ,设直角三角板的另一直角边
,设直角三角板的另一直角边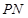 与
与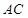 相交于点E.设
相交于点E.设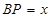 ,
,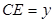 ,那么
,那么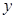 与
与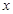 之间的函数图象大致是( )
之间的函数图象大致是( )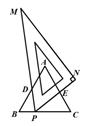
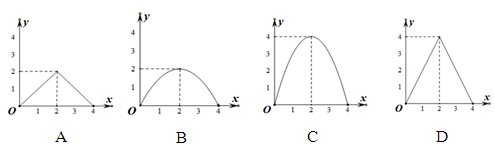
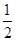 x(4-x),配方得到y=-
x(4-x),配方得到y=-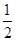 (x-2)2+2,然后根据二次函数的性质对各选项进行判断.
(x-2)2+2,然后根据二次函数的性质对各选项进行判断.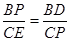 ,即
,即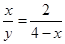 ,
,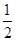 x(4-x)=-
x(4-x)=-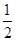 (x-2)2+2,(0≤x≤4).
(x-2)2+2,(0≤x≤4).

 目标测试系列答案
目标测试系列答案科目:初中数学 来源:不详 题型:解答题
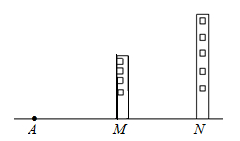
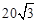 m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?
m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
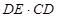
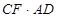 (填“<”或“=”或“>”);
(填“<”或“=”或“>”);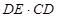 =
=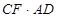 成立?并证明你的结论;
成立?并证明你的结论;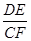 的值为 .
的值为 .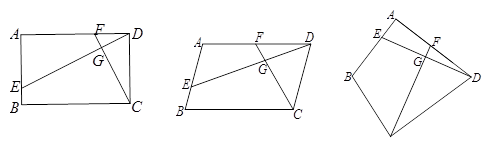
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
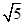 ,sinB=
,sinB=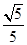 ,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.
,点P为边BC上一动点,PD∥AB,PD交AC于点D,连结AP.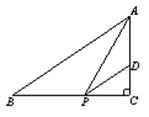
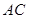 、
、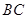 的长;
的长;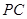 的长为
的长为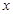 ,
,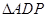 的面积为
的面积为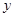 .当
.当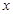 为何值时,
为何值时,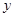 最大并求出最大值.
最大并求出最大值.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com