
【题目】结合“爱市西,爱生活,会创新”的主题,某同学设计了一款“地面霓虹探测灯”,增加美观的同时也为行人的夜间行路带去了方便.他的构想如下:在平面内,如图1所示,灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 便立即回转,灯
便立即回转,灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 便立即回转,两灯不停交叉照射巡视.若灯
便立即回转,两灯不停交叉照射巡视.若灯![]() 转动的速度是每秒2度,灯
转动的速度是每秒2度,灯![]() 转动的速度是每秒1度.假定主道路是平行的,即
转动的速度是每秒1度.假定主道路是平行的,即![]() ,且
,且![]() .
.
(1)填空:![]() ______
______![]() ;
;
(2)若灯![]() 射线先转动60秒,灯
射线先转动60秒,灯![]() 射线才开始转动,在灯
射线才开始转动,在灯![]() 射线到达
射线到达![]() 之前,
之前,![]() 灯转动几秒,两灯的光束互相平行?
灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯![]() 射线到达
射线到达![]() 之前,若射出的光束交于点
之前,若射出的光束交于点![]() ,过
,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,则在转动过程中,请探究
,则在转动过程中,请探究![]() 与
与![]() 的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.
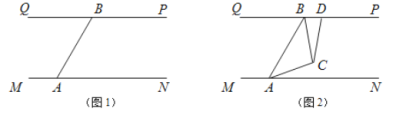
【答案】(1)120;(2)![]() 灯转动100秒,两灯的光束互相平行;(3)在转动过程中,
灯转动100秒,两灯的光束互相平行;(3)在转动过程中,![]() 和
和![]() 关系不会变化,且有
关系不会变化,且有![]() ,理由见解析.
,理由见解析.
【解析】
(1)先根据角的倍差求出![]() 的度数,再根据平行线的性质即可得;
的度数,再根据平行线的性质即可得;
(2)设A灯转动时间为t秒,先求出两个临界位置:灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 、灯
、灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() ,再分三种情况,分别利用平行线的性质列出等式求解即可得;
,再分三种情况,分别利用平行线的性质列出等式求解即可得;
(3)先根据角的和差求出![]() ,再根据三角形的内角和定理可得
,再根据三角形的内角和定理可得![]() ,然后根据角的和差可得
,然后根据角的和差可得![]() ,由此即可得.
,由此即可得.
(1)∵![]() ,
,![]()
∴![]()
![]()
![]() (两直线平行,内错角相等)
(两直线平行,内错角相等)
故答案为:120;
(2)设A灯转动时间为t秒
灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 所需时间为
所需时间为![]() (秒),灯
(秒),灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 所需时间为
所需时间为![]() (秒)
(秒)
灯![]() 射线从
射线从![]() 开始顺时针旋转至
开始顺时针旋转至![]() 所需时间为
所需时间为![]() (秒)
(秒)
则t的取值范围为![]() ,即
,即![]()
由题意,分以下三种情况:
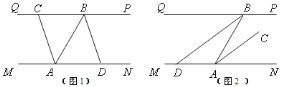
①当![]() 时,如图1所示
时,如图1所示
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
解得![]()
此时,![]()
即两灯的光束重合,不符题意,舍去
②当![]() 时,如图2所示,此时灯A射线未从AN回转
时,如图2所示,此时灯A射线未从AN回转
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
解得![]() (不符题设,舍去)
(不符题设,舍去)
③当![]() 时,如图2所示,此时灯A射线旋转至AN,并已开始回转
时,如图2所示,此时灯A射线旋转至AN,并已开始回转
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
解得![]() ,符合题设
,符合题设
综上,![]() 灯转动100秒,两灯的光束互相平行;
灯转动100秒,两灯的光束互相平行;
(3)![]() 和
和![]() 关系不会变化,且有
关系不会变化,且有![]() ,理由如下:
,理由如下:
设灯A射线转动时间为t秒
∵![]()
∴![]()
又∵![]()
∴![]()
![]()
∴![]()
∴![]() ,即
,即![]()
故在转动过程中,![]() 和
和![]() 关系不会变化,且有
关系不会变化,且有![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点 ![]() ,点
,点 ![]() .对
.对 ![]() 点作下列变换:①先 把点
点作下列变换:①先 把点 ![]() 向右平移
向右平移 ![]() 个单位,再向上平移
个单位,再向上平移 ![]() 个单位;②先把点
个单位;②先把点 ![]() 向上平移
向上平移 ![]() 个单位,再向右平移
个单位,再向右平移 ![]() 个单位;③先作点
个单位;③先作点 ![]() 以
以 ![]() 轴为对称轴的轴对称变换,再向左平移
轴为对称轴的轴对称变换,再向左平移 ![]() 个单位;④先作点
个单位;④先作点 ![]() 以
以 ![]() 轴为对称轴的轴对称变换,再向右平移
轴为对称轴的轴对称变换,再向右平移 ![]() 个单位,其中能由点
个单位,其中能由点 ![]() 得到点
得到点 ![]() 的变换 是_________。
的变换 是_________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为26.6°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)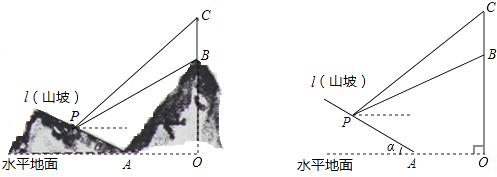
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆O是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点C作圆O的切线,交AB的延长线于点D,则∠D的度数是( ) 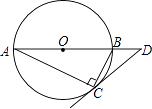
A.25°
B.40°
C.50°
D.65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把△ABC经过一定的变换得到△A′B′C′,如果△ABC边上点P的坐标为(a,b),那么这个点在△A′B′C′中的对应点P′的坐标为( )
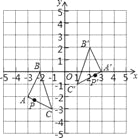
A. (﹣a,b﹣2) B. (﹣a,b+2) C. (﹣a+2,﹣b) D. (﹣a+2,b+2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1: ![]() 的坡面AB向上行走到B处,测得广告牌顶部C的仰角为45°,又知AB=10m,AE=15m,求广告牌CD的高度(精确到0.1m,测角仪的高度忽略不计)
的坡面AB向上行走到B处,测得广告牌顶部C的仰角为45°,又知AB=10m,AE=15m,求广告牌CD的高度(精确到0.1m,测角仪的高度忽略不计)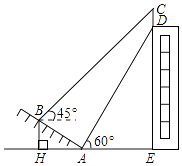
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校2000名学生每周去图书馆时间的情况,随机调查了其中的100名学生,对这100名学生每周去图书馆的时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周去图书馆的时间在6≤x<8小时的学生人数占20%.根据以上信息及统计图解答下列问题: 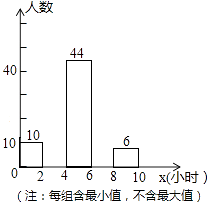
(1)本次调查属于调查,样本容量是;
(2)请补全频数分布直方图中空缺的部分;
(3)若从这100名学生中随机抽取1名学生,求抽取的这个学生每周去图书馆的时间恰好在8﹣10小时的概率;
(4)估计全校学生每周去图书馆的时间不少于6小时的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com