练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．已知一个正多边形的内角和是1800°，则这个正多边形的外角是30度．

    分析 根据多边形的内角和公式，可得多边形，根据正多边形的外角，可得答案．

    解答 解：设多边形为n边形，由题意，得
    （n-2）•180=1800，
    解得n=12，
    360÷12=30，
    故答案为：30．

    点评 本题考查了多边形的内角与外角，利用多边形的内角和与外角和是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．问题再现：
    数形结合是解决数学问题的一种重要的思想方法，借助这种方法可将抽象的数学知识变得直观起来并且具有可操作性，从而可以帮助我们快速解题．初中数学里的一些代数公式，很多都可以通过表示几何图形面积的方法进行直观推导和解释．
    例如：利用图形的几何意义证明完全平方公式．
    证明：将一个边长为a的正方形的边长增加b，形成两个矩形和两个正方形，如图1：
    这个图形的面积可以表示成：
    （a+b）2或　a2+2ab+b2
    ∴（a+b）2 =a2+2ab+b2
    这就验证了两数和的完全平方公式．
    类比解决：
    （1）请你类比上述方法，利用图形的几何意义证明平方差公式．（要求画出图形并写出推理过程）
    问题提出：如何利用图形几何意义的方法证明：13+23=32？
    如图2，A表示1个1×1的正方形，即：1×1×1=13
    B表示1个2×2的正方形，C与D恰好可以拼成1个2×2的正方形，因此：B、C、D就可以表示2个2×2的正方形，即：2×2×2=23
    而A、B、C、D恰好可以拼成一个（1+2）×（1+2）的大正方形．
    由此可得：13+23=（1+2）2=32
    尝试解决：
    （2）请你类比上述推导过程，利用图形的几何意义确定：13+23+33=62．（要求写出结论并构造图形写出推证过程）．
    （3）问题拓广：
    请用上面的表示几何图形面积的方法探究：13+23+33+…+n3=[$\frac{1}{2}$n（n+1）]2．（直接写出结论即可，不必写出解题过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．某班为奖励在校运动会上取得较好成绩的运动员，花了396元钱购买甲、乙两种奖品共30件．其中甲种奖品每件15元，乙种奖品每件12元，求甲、乙两种奖品各买多少件？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如下表：
    x…-10123…
    y…105212…
    （1）求该函数的表达式；
    （2）当y＜5时，x的取值范围是0＜x＜4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．（1）计算：（3-π）0+4sin45°-$\sqrt{8}$+|1-$\sqrt{3}$|
    （2）已知a-b=$\sqrt{2}$，求（a-2）2+b（b-2a）+4（a-1）的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

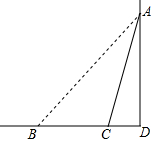    12．如图所示，一块广告牌AB顶端固定在一堵墙AD的A点处，与地面夹角∠ABD=45°，由于施工底部断裂掉一段以后，底部落在距离B点8米处的C点，此时与地面夹角∠ACD=75°．求断裂前、后的广告牌AB、AC的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：$\sqrt{9}$-${（1-\sqrt{2}）}^{0}$+|-5|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．一个锐角的补角等于这个锐角的余角的3倍，求这个锐角？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：
    摸球的次数n1001502005008001000
    摸到白球的次数m5996116290480601
    摸到白球的频率$\frac{m}{n}$a0.640.58b0.600.601
    （1）上表中的a=0.59；b=0.58
    （2）“摸到白球”的概率的估计值是0.60（精确到0.1）；
    （3）试估算口袋中黑、白两种颜色的球各有多少只？

    查看答案和解析>>

    同步练习册答案