
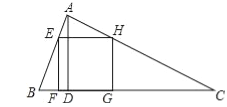
【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
【答案】(1)详见解析;(2)正方形EFGH的边长为![]() cm,面积为
cm,面积为![]() cm2.
cm2.
【解析】
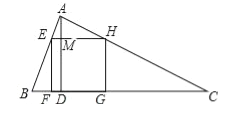
试题分析:(1)根据EH∥BC即可证明△AEH∽△ABC;(2)如图设AD与EH交于点M,易证四边形EFDM是矩形,设正方形边长为x,由(1)知△AEH∽△ABC,根据相似三角形的性质可得得![]() ,代入数据列出方程即可解决问题.
,代入数据列出方程即可解决问题.
试题解析:(1)证明:∵四边形EFGH是正方形,
∴EH∥BC,
∴∠AEH=∠B,∠AHE=∠C,
∴△AEH∽△ABC.
(2)解:如图设AD与EH交于点M.
∵∠EFD=∠FEM=∠FDM=90°,
∴四边形EFDM是矩形,
∴EF=DM,设正方形EFGH的边长为x,
∵△AEH∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴x=![]() ,
,
∴正方形EFGH的边长为![]() cm,面积为
cm,面积为![]() cm2.
cm2.


科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,把△BCD沿对角线BD折叠得到△BED,线段BE与AD相交于点P,若AB=2,BC=4. 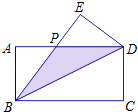
(1)BD=;
(2)点P到BD的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】9名学生的体重分别是41、48、50、53、49、53、53、51、67(单位:kg),这组数据的众数是( )
A. 41 B. 48
C. 53 D. 67
查看答案和解析>>
科目:初中数学 来源: 题型:
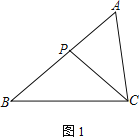
【题目】在△ABC中,P为边AB上一点.
(1) 如图1,若∠ACP=∠B,求证:AC2=AP·AB;
(2) 若M为CP的中点,AC=2,
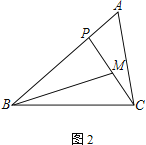
① 如图2,若∠PBM=∠ACP,AB=3,求BP的长;
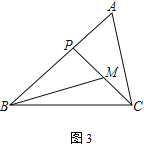
② 如图3,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,四边形OABC是矩形,点B的坐标为(4,3),反比例函数y= ![]() 的图象经过点B.
的图象经过点B. 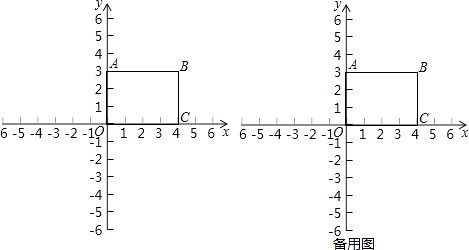
(1)求反比例函数的解析式;
(2)一次函数y=ax﹣1的图象与y轴交于点D,与反比例函数y= ![]() 的图象交于点E,且△ADE的面积等于6,求一次函数的解析式;
的图象交于点E,且△ADE的面积等于6,求一次函数的解析式;
(3)在(2)的条件下,直线OE与双曲线y= ![]() (x>0)交于第一象限的点P,将直线OE向右平移
(x>0)交于第一象限的点P,将直线OE向右平移 ![]() 个单位后,与双曲线y=
个单位后,与双曲线y= ![]() (x>0)交于点Q,与x轴交于点H,若QH=
(x>0)交于点Q,与x轴交于点H,若QH= ![]() OP,求k的值.
OP,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com