
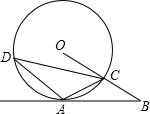
 已知,如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=$\frac{1}{2}$OB.
已知,如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=$\frac{1}{2}$OB.分析 (1)根据如果一个三角形一边上的中线等于这边的一半,这个三角形是直角三角形,即可判断∠OAB=90°,即可解决问题.
(2)只要证明∠DOA=90°,利用勾股定理即可解决问题.
解答 (1)证明:如图连接OA.
∵AC=$\frac{1}{2}$OB,OC=CB,
∴AC=OC=CB,
∴∠OAB=90°,
∴AB是⊙O的切线.
(2)解:连接OD.
∵∠DAO=2∠DCA,∠DCA=45°,
∴∠DOA=90°,∵OD=OA=OC=2,
∴AD=$\sqrt{O{D}^{2}+O{A}^{2}}$=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
点评 本题考查切线的判定、圆周角定理、勾股定理等知识,解题的关键是学会添加常用辅助线,灵活运用所学知识解决问题,属于中考常考题型.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
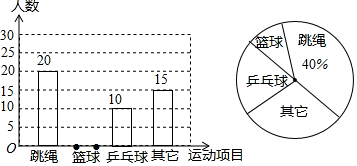
 为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.| 进球数(个) | 人数 |
| 0 | 1 |
| 1 | 2 |
| 2 | x |
| 3 | y |
| 4 | 4 |
| 5 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
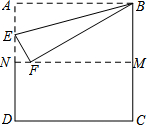 如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB的长为2,求FM的长.
如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE,若AB的长为2,求FM的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
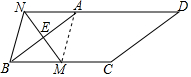 如图,在平行四边形ABCD中,AB=6,BC=8,∠ABC=30°,点E是AB边的中点,点M是BC边上的动点,连接ME并延长交DA的延长线于点N.
如图,在平行四边形ABCD中,AB=6,BC=8,∠ABC=30°,点E是AB边的中点,点M是BC边上的动点,连接ME并延长交DA的延长线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请填空完成下面的证明:
请填空完成下面的证明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com