
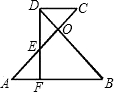
 在图中,已知AB∥CD,AO=OB,DF=FB,DF交AC于E.
在图中,已知AB∥CD,AO=OB,DF=FB,DF交AC于E.| DE |
| OE |
| EC |
| ED |
| DE |
| OE |
| EC |
| ED |


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:初中数学 来源: 题型:
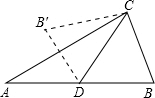 如图,在△ABC中,已知AB=2a,∠A=30°,CD是AB边的中线,若将△ABC沿CD对折起来,折叠后两个小△ACD与△BCD重叠部分的面积恰好等于折叠前△ABC的面积的
如图,在△ABC中,已知AB=2a,∠A=30°,CD是AB边的中线,若将△ABC沿CD对折起来,折叠后两个小△ACD与△BCD重叠部分的面积恰好等于折叠前△ABC的面积的| 1 |
| 4 |
| ||
| 3 |
查看答案和解析>>
科目:初中数学 来源:2009-2010学年浙江省温州市永嘉县乌牛镇中学九年级(上)第三次月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com