
【题目】如图,点 O 是等边△ABC 内一点,∠AOB=105°,∠BOC 等于α,将△BOC 绕点 C 按 顺时针方向旋转 60°得△ADC,连接 OD.
(1)求证:△COD 是等边三角形.
(2)求∠OAD 的度数.
(3)探究:当α为多少度时,△AOD 是等腰三角形?

【答案】(1)证明见解析;(2)45°;(3)105°,127.5°或 150°.
【解析】(1)由旋转的性质得到△BCO≌△ACD, 再由全等三角形对应边相等得到OC=CD,根据有一个角为60°的等腰三角形是等边三角形即可得出结论;
(2)由等边三角形的性质、三角形内角和定理以及旋转的性质即可得出结论.
(3)若△AOD 是等腰三角形 ,分三种情况讨论即可.
(1)∵△BOC 旋转 60°得到△ADC,∴△BCO≌△ACD,
∴OC=CD,且∠OCD=60°,则△OCD 是等边三角形;
(2)∵△ABC 为等边三角形,∴∠BAO+∠OAC=60°,∠ABO+∠OBC=60°.
∵∠AOB=105°,∴∠BAO+∠ABO=75°,∴∠OAC+∠OBC=120°﹣105°=45°.
∵△BOC 旋转 60°得到△ADC,∴△BCO≌△ACD,
∴∠DAC=∠OBC ,∴∠OAD=∠OAC+∠CAD=45°.
(3)若△AOD 是等腰三角形 .∵由(1)知△OCD 是等边三角形,∴∠COD=60°.
由(2)知∠OAD=45°, 分三种情况讨论:
①当 OA=OD 时,∠AOD=90°,∠α=360°﹣105°﹣60°﹣90°=105°;
②当 OA=AD 时,∠AOD=67.5°,∠α=360°﹣105°﹣60°﹣67.5°=127.5°;
③当 AD=OD 时,∠AOD=45°,∠α=360°﹣105°﹣60°﹣45°=150°.
综上所述:当α=105°,127.5°或 150°时,△AOD 是等腰三角形 .


科目:初中数学 来源: 题型:
【题目】某学校准备开展“阳光体有活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
各项目人数条形统计图 各项目人数扇形统计图


(1)这次活动一共调查了______名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择乒乓球项目的人数所在扇形的圆心角等于_____度;
(4)若该学校有![]() 人,请你估计该学校选择足球项目的学生人数约是多少人.?
人,请你估计该学校选择足球项目的学生人数约是多少人.?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个相同的红球,为了估计袋中红球的数量,某学习小组做了摸球实验,他们将30个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复![]() 下表是几次活动汇总后统计的数据:
下表是几次活动汇总后统计的数据:
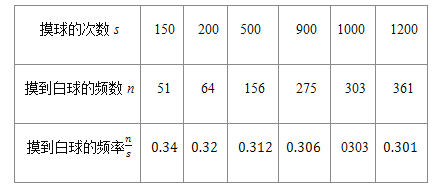
![]() 请估计:当次数s很大时,摸到白球的频率将会接近______ ;假如你去摸一次,你摸到红球的概率是______
请估计:当次数s很大时,摸到白球的频率将会接近______ ;假如你去摸一次,你摸到红球的概率是______ ![]() 精确到
精确到![]() .
.
![]() 试估算口袋中红球有多少只?
试估算口袋中红球有多少只?
![]() 解决了上面的问题后请你从统计与概率方面谈一条启示.
解决了上面的问题后请你从统计与概率方面谈一条启示.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织1000名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动.随机机取一些学生在评比中的成绩制成的统计图表如下:


根据以上图表提供的信息,解答下列问题:
(1)写出表中a、b的数值:a ,b ;
(2)补全频数分布表和频数分布直方图;
(3)如果评比成绩在95分以上(含95 分)的可以获得一等奖,试估计该校参加此次活动获得一等 奖的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古埃及人曾经用如图所示的方法画直角:把一根长绳打上等距离的13个结,然后以3个结间距、4个结间距、5个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角,这样做的道理是( )
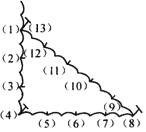
A. 直角三角形两个锐角互补
B. 三角形内角和等于180°
C. 如果三角形两条边长的平方和等于第三边长的平方
D. 如果三角形两条边长的平方和等于第三边长的平方,那么这个三角形是直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】牛奶是最古老的天然饮料之一,被誉为“白色血液”,对人体的重要性可想而知,现已成为国家营养餐计划备选食品之一.为推行国家营养餐计划,某乳品公司向某营养餐中心运输不少于![]() 的牛奶.由铁路运输每千克只需运费0.58元;由公路运输,每千克需运费0.28元,还需其他费用600元.请探究并说明选用哪种运输方式所需费用较少?
的牛奶.由铁路运输每千克只需运费0.58元;由公路运输,每千克需运费0.28元,还需其他费用600元.请探究并说明选用哪种运输方式所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
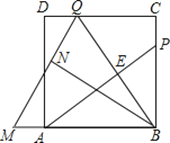
【题目】如图,P为正方形ABCD的边BC上一动点(P与B.C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
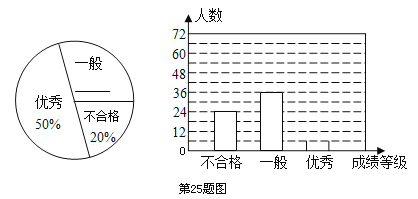
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有______人达标;
(3)若该校学生有1000人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
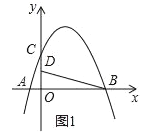
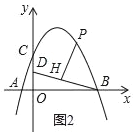
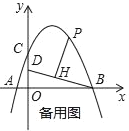
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+4交x轴于点A(﹣2,0)和B(B在A右侧),交y轴于点C,直线y=![]() 经过点B,交y轴于点D,且D为OC中点.
经过点B,交y轴于点D,且D为OC中点.
(1)求抛物线的解析式;
(2)若P是第一象限抛物线上的一点,过P点作PH⊥BD于H,设P点的横坐标是t,线段PH的长度是d,求d与t的函数关系式;
(3)在(2)的条件下,当d=![]() 时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
时,将射线PH绕着点P顺时针方向旋转45°交抛物线于点Q,求点Q的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com