
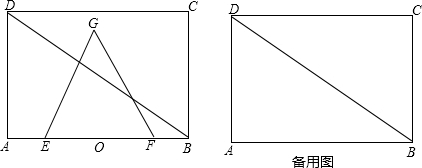
分析 (1)当等边△EFG的顶点G恰好落在CD上时,OG=BC,根据直角三角形性质可得EO=4,即可求得t值;
(2)按照等边△EFG和矩形ABCD重叠部分的图形特点,分为0≤t<4,4≤t<6,6≤t<10,10≤t<14,14≤t<18五种情况,分别写出函数关系式;
(3)存在.当△AOH是等腰三角形时,分为AH=AO=3,HA=HO,OH=OA三种情况,分别画出图形,根据特殊三角形的性质,列方程求t的值
解答 解:(1)当等边△EFG的顶点G恰好落在CD上时,
∵点O是EF的中点
∴OG=BC=4$\sqrt{3}$,
∵在△EOG中,∠EGO=30°,
∴$\frac{EO}{GO}=\frac{1}{\sqrt{3}}$,
∴EO=4
∴t=4s时,等边△EFG的顶点G恰好落在CD上.
(2)①当点G在矩形ABCD内部及在边长CD上这段时间,即t在0-4s,重叠部分的面积为△EFG的面积,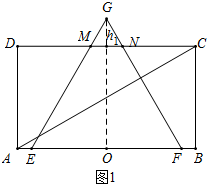
设△EFG的高为h,
根据已知可得,EF=2t,h=$\sqrt{3}$t,
故S△GEF=$\frac{1}{2}$•EF•h=$\frac{1}{2}$•2t•($\sqrt{3}$t)=$\sqrt{3}$t2,(0≤t<4),
②如图1,当点G在矩形ABCD外部,点E运动到点A这段时间,即t在4-6s(AO=6),
设EG、FG分别与CD交于点M,N,△GMN的高为h1,
则h1=h-BC=$\sqrt{3}$t-4$\sqrt{3}$,
易得△GMN∽△GEF,
∴$\frac{S△GMN}{S△GEF}=\frac{{{h}_{1}}^{2}}{{h}^{2}}$,
∴S△GMN=$\sqrt{3}$t2•$\frac{(\sqrt{3}t-4\sqrt{3})^{2}}{(\sqrt{3}t)^{2}}$=$\sqrt{3}$(t-4)2=$\sqrt{3}$(t-4)2,
∴S四边形EMNF=S△GEF-S△GMN=$\sqrt{3}$t2-$\sqrt{3}$(t-4)2=8$\sqrt{3}$t-16$\sqrt{3}$,(4≤t<6),
③当点E到达A点时,F正好在B点,此时等边△GEF图形不再变化,保持向右平移,故重叠面积仍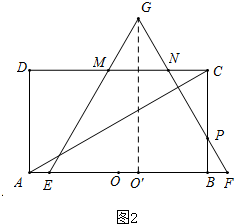 为S五边形EMNPB,直到点N与C点重合,如图2.
为S五边形EMNPB,直到点N与C点重合,如图2.
设FG与BC交于点P,EF中点为O′,△GMN中的高为h2,连接O′G,
∵在等边△EFG中,EF=12,
∴O′F=6,GO′=6$\sqrt{3}$,
∵在Rt△BPF中,∠BPF=∠O′GF=30°,
∴$\frac{BF}{PB}=\frac{1}{\sqrt{3}}$,
∵BF=AE=t-6,
∴PB=$\sqrt{3}$(t-6),
∵h2=GO′-BC=6$\sqrt{3}$-4$\sqrt{3}$=2$\sqrt{3}$,
∴MN=4,
∴S=S梯形EMNF-S△BPF=$\frac{1}{2}$•(4+12)•4$\sqrt{3}$-$\frac{1}{2}$•(t-6)•$\sqrt{3}$(t-6)=-$\frac{\sqrt{3}}{2}$t2+6$\sqrt{3}$t+14$\sqrt{3}$
当点N与C点重合时,PB=BC,
即:4$\sqrt{3}$=$\sqrt{3}$(t-6),
∴t=10s,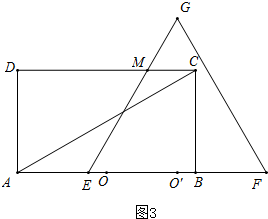
故6≤t<10,重叠面积为=-$\frac{\sqrt{3}}{2}$t2+6$\sqrt{3}$t+14$\sqrt{3}$.
④点E继续移动,点M与点C重合前这段时间,重叠面积为S四边形EBCM,如图3,
当点M与点C重合时,EB=4,AE=8,
运动总时间为8+6=14s
即10≤t<14,
由图可知,EB=t-10,
易得等边△GCM的高为2$\sqrt{3}$,
即CM=4,
故S四边形EBCM=$\frac{1}{2}$•(4+t-10)•4$\sqrt{3}$=2$\sqrt{3}$t-12$\sqrt{3}$(10<t≤14),
⑤点E继续移动,重叠面积为S△EBQ,直到点E与点B重合,设EG与BC相交于点Q,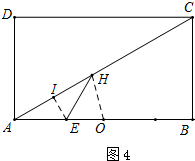
EB=t-14,易得EQ=$\sqrt{3}$(t-14),
S△EBC=$\frac{1}{2}$•(t-14)•$\sqrt{3}$(t-14)=$\frac{\sqrt{3}}{2}$(t-14)2,(14≤t<18),
综上所述,S=$\left\{\begin{array}{l}{\sqrt{3}{t}^{2}(0≤t<6)\\;\\;}\\{8\sqrt{3}t-16\sqrt{3}(4≤t<10)}\\{-\frac{\sqrt{3}}{2}{t}^{2}+6\sqrt{3}t+14\sqrt{3}(6≤t<10)}\\{2\sqrt{3}t-12\sqrt{3}(10≤t<14)}\\{\frac{\sqrt{3}}{2}(t-14)^{2}(14≤t<18)}\end{array}\right.$
(3)t=6-2$\sqrt{3}$或6+2$\sqrt{3}$或t=4或t=8或t=12
理由如下:
在Rt△ABC中,tan∠CAB=$\frac{BC}{AB}$=$\frac{\sqrt{3}}{3}$,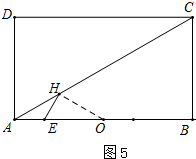
∴∠CAB=30°,
又∵∠HEO=60°,
∴∠HAE=∠AHE=30°,
∴AE=HE=6-t或t-6,
①当AH=AO=6时,(如图4),过点E作EI⊥AH于I,
则AI=$\frac{1}{2}$AH=3,
在Rt△AIE中,cos∠IAE=$\frac{AI}{AE}$,即cos30°=$\frac{3}{AE}$,
∴AE=2$\sqrt{3}$,即6-t=2$\sqrt{3}$或t-6=2$\sqrt{3}$,∴t=6-2$\sqrt{3}$或6+2$\sqrt{3}$,
②当HA=HO时,(如图5)则∠HOA=∠HAO=30°,
又∵∠HEO=60°,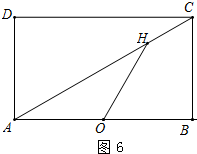
∴∠EHO=90°,EO=2HE=2AE,
又∵AE+EO=6,
∴AE+2AE=6,AE=2,
即6-t=2或t-6=2,
∴t=4s或t=8s;
③当OH=OA时,则∠OHA=∠OAH=30°,
∴∠HOB=60°=∠HEB,
∴点E和点O重合,
∴AE=AO=6,
∴t=6+6=12s;
综上所述,存在5个这样的t值,使△AOH是等腰三角形,即t=6-2$\sqrt{3}$或6+2$\sqrt{3}$或t=4或t=8或t=12.
点评 本题考查了特殊三角形、矩形的性质,相似三角形的判定与性质,解直角三角形的有关知识.关键是根据特殊三角形的性质,分类讨论.


科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
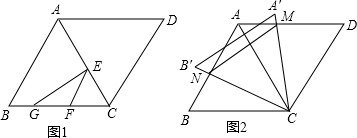
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
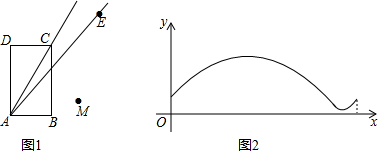
| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
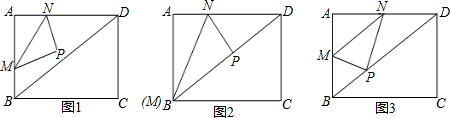
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 正方形四条边相等 | |
| C. | 数据1,3,6,1,2,2的众数是2 | |
| D. | 检验航天飞机的零部件是否合格适用全面调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.124×10-2 | B. | 1.24×10-3 | C. | 1.24×103 | D. | 1.24×102 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com