
【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0)、C(0,﹣3).
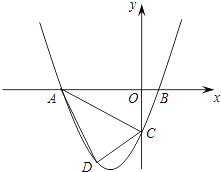
(1)求抛物线的解析式.
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?如存在,求点P的坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2+
x2+![]() x﹣3(2)
x﹣3(2)![]() (3)P1(﹣3,﹣3)或P2(
(3)P1(﹣3,﹣3)或P2(![]() ,3)或P3(
,3)或P3(![]() ,3)
,3)
【解析】
(1)把点B(1,0)、C(0,﹣3)标代入抛物线y=ax2+3ax+c求出a,c的值即可;
(2)过点D作DE∥y轴交AC于E,利用待定系数法求出直线AC的解析式,故可得出DE=﹣![]() (m+2)2+3,,再由当m=﹣2时,DE有最大值为3,此时,S△ACD有最大值,从而可求出结论;
(m+2)2+3,,再由当m=﹣2时,DE有最大值为3,此时,S△ACD有最大值,从而可求出结论;
(3) ①过点C作CP1∥x轴交抛物线于点P1,过点P1作P1E1∥AC交x轴于点E1 ,此时四边形ACP1E1为平行四边形,根据PC两点的纵坐标相等可得出P点坐标;②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,令P(x,3),由![]() x2+
x2+ ![]() x﹣3=3,得出x的值即可得出P点坐标.
x﹣3=3,得出x的值即可得出P点坐标.
(1)解:将点B、C的坐标代入抛物线的解析式得: ![]() ,
,
解得:a= ![]() ,c=﹣3.
,c=﹣3.
∴抛物线的解析式为y= ![]() x2+
x2+ ![]() x﹣3.
x﹣3.
(2)解:令y=0,则 ![]() x2+
x2+ ![]() x﹣3=0,解得x1=1,x2=﹣4,
x﹣3=0,解得x1=1,x2=﹣4,
∴A(﹣4,0)、B(1,0).
令x=0,则y=﹣3,
∴C(0,﹣3),
∴S△ABC= ![]() ×5×3=
×5×3= ![]() .
.
设D(m, ![]() m2+
m2+ ![]() m﹣3),
m﹣3),
过点D作DE∥y轴交AC于E.直线AC的解析式为y=﹣ ![]() x﹣3,则E(m,﹣
x﹣3,则E(m,﹣ ![]() m﹣3),
m﹣3),
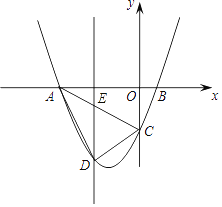
DE=﹣ ![]() m﹣3﹣(
m﹣3﹣( ![]() m2+
m2+ ![]() m﹣3)=﹣
m﹣3)=﹣ ![]() (m+2)2+3,
(m+2)2+3,
当m=﹣2时,DE有最大值为3,
此时,S△ACD有最大值为 ![]() ×DE×4=2DE=6.
×DE×4=2DE=6.
∴四边形ABCD的面积的最大值为6+ ![]() =
= ![]() ,
,
(3)解:如图所示:

①过点C作CP1∥x轴交抛物线于点P1 , 过点P1作P1E1∥AC交x轴于点E1 , 此时四边形ACP1E1为平行四边形,
∵C(0,﹣3),
∴设P1(x,﹣3),
∴ ![]() x2+
x2+ ![]() x﹣3=﹣3,
x﹣3=﹣3,
解得x1=0,x2=﹣3,
∴P1(﹣3,﹣3);
②平移直线AC交x轴于点E,交x轴上方的抛物线于点P,当AC=PE时,四边形ACEP为平行四边形,
∵C(0,﹣3),
∴设P(x,3),
∴ ![]() x2+
x2+ ![]() x﹣3=3,
x﹣3=3,
解得x= ![]() 或x=
或x= ![]() ,
,
∴P2( ![]() ,3)或P3(
,3)或P3( ![]() ,3),
,3),
综上所述存在3个点符合题意,坐标分别是P1(﹣3,﹣3)或P2( ![]() ,3)或P3(
,3)或P3( ![]() ,3).
,3).


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】某市为解决农村燃气困难,在P处建立了一个燃气站,从P站分别向A、B、C村铺设燃气管道。已知B村在A村的北偏东60°方向,距离A村2.4km,C村在A村的正东方向,距离A村1.8km,要使此工程费用最省,管道PA+PB+PC之和需最短,则最短长度为______________km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE、CF分别是钝角△ABC(∠A>90°)的高,在BE上截取BP=AC,在CF的延长线截取CQ=AB,连结AP、AQ,请推测AP与AQ的数量和位置关系并加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,连结CP并延长CP交AD于Q点.给出以下结论:
①四边形AECF为平行四边形;
②∠PBA=∠APQ;
③△FPC为等腰三角形;
④△APB≌△EPC.
其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究
(1)在 6 月份的日历中(如图 1),任意圈出一列上相邻的三个数,设中间的一个数为 a,则用含 a 的代数式表示这三个数(从小到大)分别是________________________________ .
(2)连续的自然数 1 至 2004 按图中的方式派成一个长方形阵列,用一个正方形框出 16 个数(如图2)
①图2中框出的这 16 个数之和是____________;
②在图2中,要使一个正方形框出的 16 个数之和分别等于 839、2000,是否可能?若不可能,试说明理由.若有可能,请求出该正方形框出的 16 个数中的最小数与最大数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成ABCD,DC与y轴的交点为E(0,6),试求a的值.
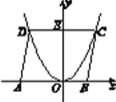
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图象解一元二次方程x2-2x-1=0时,我们采用的一种方法是在直角坐标系中画出抛物线y=x2和直线y=2x+1,两图象交点的横坐标就是该方程的解.
(1)请再给出一种利用图象求方程x2-2x-1=0的解的方法;
(2)已知函数y=x3的图象(如图),求方程x3-x-2=0的解(结果保留两位有效数字).
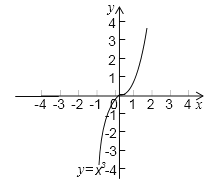
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】合肥市某学校搬迁,教师和学生的寝室数量在增加,若该校今年准备建造三类不同的寝室,分别为单人间(供一个人住宿),双人间(供两个人住宿),四人间(供四个人住宿).因实际需要,单人间的数量在20至30之间(包括20和30),且四人间的数量是双人间的5倍.
(1)若2015年学校寝室数为64个,2017年建成后寝室数为121个,求2015至2017年的平均增长率;
(2)若建成后的寝室可供600人住宿,求单人间的数量;
(3)若该校今年建造三类不同的寝室的总数为180个,则该校的寝室建成后最多可供多少师生住宿?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com