
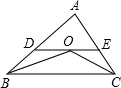
 如图,在△ABC中,∠ABC与∠ACB的角平分线相交于点O.
如图,在△ABC中,∠ABC与∠ACB的角平分线相交于点O.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
 如图所示的两个转盘中,指针落在每一个扇形的机会均等,小英和小丽用两个转盘做“配紫色”游戏,若配成紫色小英得胜,否则小丽得胜,这个游戏规则对双方公平吗?(红色+蓝色=紫色,配成紫色者胜)
如图所示的两个转盘中,指针落在每一个扇形的机会均等,小英和小丽用两个转盘做“配紫色”游戏,若配成紫色小英得胜,否则小丽得胜,这个游戏规则对双方公平吗?(红色+蓝色=紫色,配成紫色者胜)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,点P是x轴上的一个动点,连结AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.当点P运动到点(
如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,3),点B在第一象限,点P是x轴上的一个动点,连结AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.当点P运动到点(| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2,请填写AE∥PF的理由.
如图,点P在CD上,已知∠BAP+∠APD=180°,∠1=∠2,请填写AE∥PF的理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com