【题目】(1)如图①，已知△ABC为直角三角形，∠A＝90°，若沿图中虚线剪去∠A，则∠1＋∠2等于( )
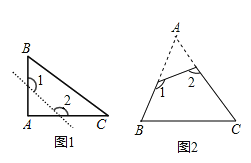
A．90° B．135° C．270° D．315°
(2)如图②，已知△ABC中，∠A＝40°，剪去∠A后成四边形，则∠1＋∠2＝________°；
(3)根据(1)与(2)的求解过程，请你归纳猜想∠1＋∠2与∠A的关系是______________．
【答案】（1）C；（2）220；（3）∠1＋∠2＝180°＋∠A.
【解析】
（1）利用了四边形内角和为360°和直角三角形的性质求解；
（2）根据三角形的外角等于与它不相邻的两个内角和求解；
（3）根据（1）（2）可以直接写出结果；
解：(1)∵四边形的内角和为360°，直角三角形中两个锐角的和为90°，
∴∠1＋∠2＝360°－(∠C＋∠B)＝360°－90°＝270°.
故选C.
(2)在△ABC中，∠A＝40°，
∠C＋∠B＝180°－40°=140°
∴∠1＋∠2＝360°－(∠C＋∠B)＝220°，
故答案是：220.
(3) 根据（1）（2）的结果可得：∠1＋∠2＝180°＋∠A
故答案是：∠1＋∠2＝180°＋∠A
互动课堂系列答案
激活思维智能训练课时导学练系列答案科目：初中数学 来源： 题型：
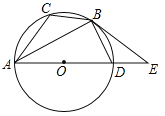
【题目】如图，已知⊙O是△ABC的外接圆，AD是⊙O的直径，且BD=BC，延长AD到E，BE是⊙O的切线，B是切点．
（1）求证：∠EBD=∠CAB；
（2）若BC=
，AC=5，求sin∠CBA．
查看答案和解析>>
科目：初中数学 来源： 题型：
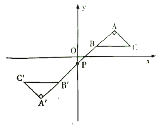
【题目】如图，在平面直角坐标系中，
的顶点
在第一象限，点
、
的坐标分别为
、
，
，
，直线
交
轴于点
，若与
关于点成中心对称，则点
的坐标为（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中数学 来源： 题型：
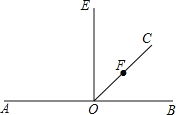
【题目】如图，O为直线AB上一点，F为射线OC上一点，OE⊥AB．
（1）用量角器和直角三角尺画∠AOC的平分线OD，画FG⊥OC，FG交AB于点G；
（2）在（1）的条件下，比较OF与OG的大小，并说明理由；
（3）在（1）的条件下，若∠BOC＝40°，求∠AOD与∠DOE的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把 6个相同的小正方体摆成如图的几何体．
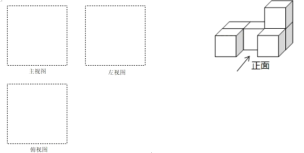
（1）画出该几何体的主视图、左视图、俯视图；
（2）如果每个小正方体棱长为
，则该几何体的表面积是 
．
（3）如果在这个几何体上再添加一些相同的小正方体，并并保持左视图和俯视图不变，那么最多可以再 添加 个小正方体．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
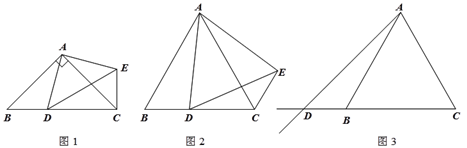
（1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE= 度；
（2）设∠BAC= 
，∠DCE= 
．
① 如图2，当点D在线段CB上，∠BAC≠90°时，请你探究
与
之间的数量关系，并证明你的结论；
② 如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时
与
之间的数量关系（不需证明）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，已知AB=8cm，BC=10cm，折叠矩形的一边AD，使点D落在BC边上的点F处，折痕为AE．以点A为原点，分别以AD所在的直线为x轴，AB所在的直线为y轴建立坐标系.
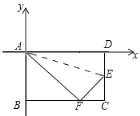
（1）写出点B、D、E、F的坐标；
（2）在坐标轴上是否存在点G，使△AFG是以AF为腰长的等腰三角形？若存在，请求出点G的坐标；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
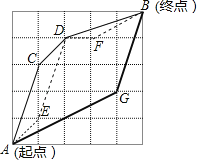
【题目】嘉嘉参加机器人设计活动，需操控机器人在5×5的方格棋盘上从A点行走至B点，且每个小方格皆为正方形，主办单位规定了三条行走路径R1，R2，R3，其行经位置如图与表所示：
路径 | 编号 | 图例 | 行径位置 |
第一条路径 | R1 | _ | A→C→D→B |
第二条路径 | R2 | … | A→E→D→F→B |
第三条路径 | R3 | ▂ | A→G→B |
已知A、B、C、D、E、F、G七点皆落在格线的交点上，且两点之间的路径皆为直线，在无法使用任何工具测量的条件下，请判断R1、R2、R3这三条路径中，最长与最短的路径分别为何？请写出你的答案，并完整说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
