利用不等式的基本性质,把下列不等式化成“x>a”或“x<a”的形式,并将解集在数轴上表示出来:
(1)x-1<-2 (2 )-2x≤6.
解:(1)根据不等式性质1,不等式两边都加上1,不等号的方向不变,得x-1+1<-2+1,即x<-1.
这个不等式的解集在数轴上的表示,如图:
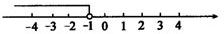
(2)根据不等式的性质3,不等式两边同除以-2(或乘以-

),不等号的方向改变,得-2x÷(-2)≥6÷(-2),即x≥-3.
这个不等式的解集在数轴上的表示,如图
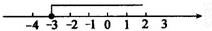
分析:解题关键是选准用哪条性质,逐步化成“x>a”或“x<a”的形式.另外,在数轴上表示解集时,一定要细心,否则极易出错.
点评:在数轴上表示不等式的解集时,可这样记忆:>向右拐,<向左拐,有“等号”实心,无“等号”空心.此外,画数轴时不要少了三要素:原点、正方向和单位长度.
