
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� ���ݷ��������������ʶԢٽ����жϣ�������Ч���ֵĶ���Ԣڽ����жϣ�����ֱ����Բ��λ�ù�ϵ�Ԣ۽����жϣ�����six120��=$\frac{1}{2}$�Ԣܽ����жϣ����ݷ�ʽ���̵Ľ�Ԣݽ����жϣ����������ֵΪ31ʱ���Ա�����ֵ��Ȼ����ݶ��κ���������ȷ��t��ֵ��
��� �⣺��֪ab=4����-2��b��1��b��0����a��ȡֵ��Χ��-2��a��0��0��a��4�����Ԣٴ���
����10240����3����Ч����Ӧ��ʾΪ1.02��104�����Ԣڴ���
��Rt��ABC�У���C=90�㣬AC=3��BC=4������C��ΪԲ�ģ�rΪ�뾶������Բ��б��ABֻ��һ�������㣬��r=$\frac{12}{5}$��3��r��4�����Ԣ۴���
����ABC�У�sinA=$\frac{1}{2}$�����A=30���150�㣬���Ԣܴ���
������x�ķ�ʽ����$\frac{x-1}{x-2}=\frac{m}{x-2}$+2�Ľ�Ϊ��������m��3��m��1�����Ԣݴ���
���κ���y=2x2+4x+1�ĶԳ���Ϊֱ��x=-1��2x2+4x+1=31�����x1=-5��x2=3����-5��t��3��1��t��3ʱ�����κ��������ֵΪ31������t��ֵΪ1��-5�����Ԣ�Ϊ�����⣮
��ѡB��
���� ���⿼���������붨�����ж�һ���������䣬�������⣮�������ⶼ��������ͽ�����������ɣ���������֪�������������֪�����Ƴ������һ���������д�ɡ��������ô������ʽ�� ��Щ�������ȷ����������֤ʵ�ģ����������������������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
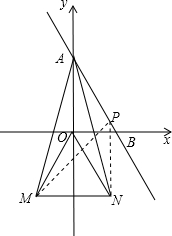 ��ͼ��ֱ��y=kx+2��0��|k|��1���ֱ��������ύ��A��B���㣬�ȱߡ�MNO����y��Գƣ���M��-1��$-\sqrt{3}$����P��ֱ��AB�ϵĶ��㣮��MAN����Ϊ30�㣬����MPN=��MANʱ����P������Ϊ$��\frac{-4k}{{k}^{2}+1}��\frac{2-2{k}^{2}}{{k}^{2}+1}��$ ��A����⣩��
��ͼ��ֱ��y=kx+2��0��|k|��1���ֱ��������ύ��A��B���㣬�ȱߡ�MNO����y��Գƣ���M��-1��$-\sqrt{3}$����P��ֱ��AB�ϵĶ��㣮��MAN����Ϊ30�㣬����MPN=��MANʱ����P������Ϊ$��\frac{-4k}{{k}^{2}+1}��\frac{2-2{k}^{2}}{{k}^{2}+1}��$ ��A����⣩���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����������У�����ʼ�����xֵΪ24�����Ƿ��ֵ�1������Ľ��Ϊ 12����2������Ľ��Ϊ6������2012������Ľ��Ϊ6��
��ͼ��ʾ����������У�����ʼ�����xֵΪ24�����Ƿ��ֵ�1������Ľ��Ϊ 12����2������Ľ��Ϊ6������2012������Ľ��Ϊ6���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3.039��101 | B�� | 3.039��104 | C�� | 3.039��105 | D�� | 30.39��104 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
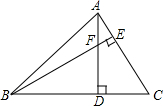 ��ͼ���ڡ�ABC�У���ABC=45�㣬AC=5��F�Ǹ�AD��BE�Ľ��㣬��BF�ij��ǣ�������
��ͼ���ڡ�ABC�У���ABC=45�㣬AC=5��F�Ǹ�AD��BE�Ľ��㣬��BF�ij��ǣ�������| A�� | 7 | B�� | 6 | C�� | 5 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��$\frac{3}{2}$ | B�� | x=$\frac{3}{2}$ | C�� | x��$\frac{3}{2}$ | D�� | x��$\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com