
、阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
②归纳:考察点的个数和可连成直线的条数 发现:如下表
发现:如下表
|
点的个数 |
可作出直线条数 |
|
2 |
1= |
|
3 |
3= |
|
4 |
6= |
|
5 |
10= |
|
…… |
…… |
|
n |
|
③推理:平面上有n个点,两点确定一条直线。取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即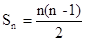
④结论: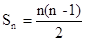
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数 ,发现:(填下表)
,发现:(填下表)
|
点的个数 |
可连成三角形个数 |
|
3 |
|
|
4 |
|
|
5 |
|
|
…… |
|
|
n |
|
(3)推理:
(4)结论:
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:阅读理解
| 点的个数 | 可作出直线条数 | ||
| 2 | 1=S2=
| ||
| 3 | 3=S3=
| ||
| 4 | 6=S4=
| ||
| 5 | 10=S5=
| ||
| … | … | ||
| n | Sn=
|
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| … | |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
| 2×1 |
| 2 |
| 3×2 |
| 2 |
| 4×3 |
| 2 |
| 2×1 |
| 2 |
| 3×2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
、阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
②归纳:考察点的个数和可连成直线的条数![]() 发现:如下表
发现:如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1= |
| 3 | 3= |
| 4 | 6= |
| 5 | 10= |
| …… | …… |
| n |
|
③推理:平面上有n个点,两点确定一条直线。取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即![]()
④结论:![]()
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数![]() ,发现:(填下表)
,发现:(填下表)
| 点的个数 | 可连成三角形个数 |
| 3 |
|
| 4 |
|
| 5 |
|
| …… |
|
| n |
|
(3)推理:
(4)结论:
查看答案和解析>>
科目:初中数学 来源:2014届人教版初一第一学期期末考试数学卷 题型:选择题
(1)阅读下列材料并填空
例:解方程  +
+ =5
=5
解:① 当x<-3时,x+2<0 ,x+3<0,
所以 =-x-2,
=-x-2, =-x-3
=-x-3
所以原方程可化为 (1) =5
解得 x= (2)
② 当-3≤x <-2时 ,x+2<0 ,x+3≥0,
所以 =-x-2,
=-x-2, =x+3
=x+3
所以原方程可化为 -x-2+x+3=5
1=5
所以此时原方程无解
③ 当x≥-2时 ,x+2≥0 ,x+3>0,
所以  = (3) ,
= (3) , = (4)
= (4)
所以原方程可化为 (5) =5
解得 x= (6)
(2)用上面的解题方法解方程
 -
- =x-6
=x-6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com