证明:连接BD、BE、DF,
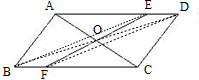
在四边形ABCD中,
∵AB=CD,AD=BC,
∴四边形ABCD是平行四边形,
∴AC和BD交点是AC、BD的中点,
同理四边形BEDF也是平行四边形,
EF和BD的交点是EF,BD的中点因两点都是BD的中点,
所以两点重合,即O为AC的中点.
分析:首先连接BD、BE、DF,根据题干条件AB=CD,AD=BC,则可以判断出四边形ABCD是平行四边形,进而知AC和BD交点是AC、BD的中点,然后根据三角形的全等证明BE=DF,进而求出四边形BEDF也是平行四边形,故知EF和BD的交点是EF,BD的中点因两点都是BD的中点,于是证得两点重合,即O为AC的中点.
点评:本题主要考查平行四边形的判定与性质和全等三角形的判定与性质的知识点,解答本题的关键是熟练掌握平行四边形判定定理,此题难度不大.

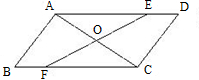 在四边形ABCD中,AB=CD,AD=BC,DE=BF,EF与对角线AC相交于O,求证:O为AC的中点.
在四边形ABCD中,AB=CD,AD=BC,DE=BF,EF与对角线AC相交于O,求证:O为AC的中点.

