
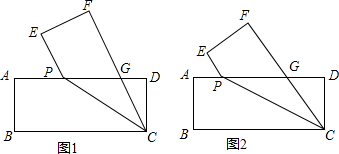
分析 (1)设PG=a,则在RT△DGC中,CG=a,DG=3-a,CD=2,利用勾股定理即可解决问题.
(2)在RT△DGC中,CD2+DG2=CG2,得到(y-x)2+22=(5-y)2,由此即可解决问题.
(3)如图1中,分两种情形讨论即可,①MG=MP,只要证明△APB≌△DGC,得到AP=DG,列出方程即可,②MG=PG,只要证明△ABP,△DPC,△BPC均为直角三角形,根据AP2+AB2+DP2+CD2=BC2,列出方程即可.
解答 (1)由题意得:四边形ABCP与四边形EFCP全等.
∴∠BCP=∠FCP.
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BCP=∠DPC,
∴∠DCP=∠FCP,
∴PG=CG,
设PG=a,
则在RT△DGC中,CG=a,DG=3-a,CD=2,且CD2+DG2=CG2,
∴22+(3-a)2=a2,解得:a=$\frac{13}{6}$,
即PG=$\frac{13}{6}$.
(2)由题意得:CF=BC=5,
∴CG=5-y,
∴PG=5-y,
∴DG=5-(5-y)-x=y-x,
∵在RT△DGC中,CD2+DG2=CG2,
∴(y-x)2+22=(5-y)2,
∴y=$\frac{21-{x}^{2}}{10-2x}$,
∴y关于x的函数解析式为:y=$\frac{21-{x}^{2}}{10-2x}$,(0<x≤3)
(3)∵△PGM是以MG为腰的等腰三角形,
∴MG=MP或MG=PG,如图1中,
①当MG=MP时,
∵∠MPG=∠MGC,
∵∠APB=∠MPG,∠MGP=∠DGC,
∴∠APB=∠DGC,
在△APB和△DGC中,
$\left\{\begin{array}{l}{∠A=∠D}\\{∠APB=∠DGC}\\{AB=DC}\end{array}\right.$,
∴△APB≌△DGC,
∴AP=DG,
∴y=2x,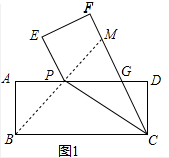
∴$\frac{21-{x}^{2}}{10-2x}$=2x,化简整理得:3x2-20x+21=0,解得:x=$\frac{10±\sqrt{37}}{3}$,
∵x=$\frac{10+\sqrt{37}}{3}$>3不符合题意舍去,
∴x=$\frac{10-\sqrt{37}}{3}$.
②当MG=PG时,
∵∠MPG=∠PMG,
∵∠MPG=∠MBC,
∴∠MBC=∠PMC,
∴CM=CB,(即点M与点F重合).
又∵∠BCP=∠MCP,
∴CP⊥BP,
∴△ABP,△DPC,△BPC均为直角三角形.
∴AP2+AB2+DP2+CD2=BC2,即x2+22+(5-x)2+22=52,
化简整理得:x2-5x+4=0,解得:x=1或4.
∵x=4>3不符合题意舍弃,
∴x=1.
补充:由PG=FG可得y-5=y,y=$\frac{5}{2}$,代入(2)中关系式即可求出x.
综上所述:当△PGM是以MG腰2的等腰三角形时,AP=$\frac{10-\sqrt{37}}{3}$或1.
点评 本题考查四边形综合题、全等三角形的判定和性质、勾股定理等知识,解题的关键是设参数利用勾股定理构建方程,学会分类讨论,注意考虑问题要全面,不能漏解,属于中考压轴题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
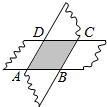 如图,用两张等宽的纸条交叉叠放在一起,重叠部分为四边形ABCD,它是一个特殊的四边形.
如图,用两张等宽的纸条交叉叠放在一起,重叠部分为四边形ABCD,它是一个特殊的四边形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 个 | B. | 1个 | C. | 2 个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
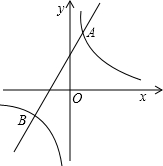 如图,直线y=x+m和双曲线y=$\frac{k}{x}$相交于点A(1,2)和点B(n,-1).
如图,直线y=x+m和双曲线y=$\frac{k}{x}$相交于点A(1,2)和点B(n,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2000(22-x)=2×1200x | B. | 2×2000(22-x)=1200x | ||
| C. | 1200(22-x)=2×2000x | D. | 2×1200(22-x)=2000x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
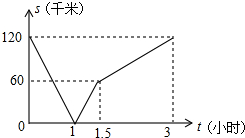 甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:干米),甲行驶的时间为s(单位:小时),s与t之间的函数关系如图所示,有下列结论:(汽车速度大于摩托车速度).①出发1小时,甲、乙在途中相遇;②出发1.5小时,甲行驶了60千米;③出发2小时,甲、乙相距8O干米;④出发3小时,甲、乙同时到达目的地;其中,正确结论的个数是( )
甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:干米),甲行驶的时间为s(单位:小时),s与t之间的函数关系如图所示,有下列结论:(汽车速度大于摩托车速度).①出发1小时,甲、乙在途中相遇;②出发1.5小时,甲行驶了60千米;③出发2小时,甲、乙相距8O干米;④出发3小时,甲、乙同时到达目的地;其中,正确结论的个数是( )| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com