
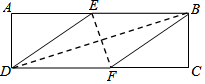
 ‘ΎΨΊ–ΈABCD÷–Θ§”–“ΜΗωΝβ–ΈBFDEΘ®ΒψEΓΔFΖ÷±π‘ΎœΏΕΈABΘ§CD…œΘ©Θ§Φ«ΥϋΟ«ΒΡΟφΜΐΖ÷±πΈΣSΨΊ–ΈABCDΚΆSΝβ–ΈBEDFΘ§»τSABCDΚΆSBFDEΘ§Ηχ≥ω»γœ¬Ϋα¬έΘΚΔΌ»τ$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$Θ§‘ρtanΓœEDF=$\frac{\sqrt{3}}{3}$ΘΜ
‘ΎΨΊ–ΈABCD÷–Θ§”–“ΜΗωΝβ–ΈBFDEΘ®ΒψEΓΔFΖ÷±π‘ΎœΏΕΈABΘ§CD…œΘ©Θ§Φ«ΥϋΟ«ΒΡΟφΜΐΖ÷±πΈΣSΨΊ–ΈABCDΚΆSΝβ–ΈBEDFΘ§»τSABCDΚΆSBFDEΘ§Ηχ≥ω»γœ¬Ϋα¬έΘΚΔΌ»τ$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$Θ§‘ρtanΓœEDF=$\frac{\sqrt{3}}{3}$ΘΜ| AΘ° | ΔΌ «ΦΌΟϋΧβΘ§ΔΎ «ΦΌΟϋΧβ | BΘ° | ΔΌ «’φΟϋΧβΘ§ΔΎ «’φΟϋΧβ | ||
| CΘ° | ΔΌ «ΦΌΟϋΧβΘ§ΔΎ «’φΟϋΧβ | DΘ° | ΔΌ «’φΟϋΧβΘ§ΔΎ «ΦΌΟϋΧβ |
Ζ÷Έω ΔΌ”…“―÷Σœ»«σ≥ωcosΓœBFC=$\frac{\sqrt{3}}{2}$Θ§‘Ό«σ≥ωtanΓœEDFΘ§Φ¥Ω…≈–ΕœΘΜ
ΔΎ”…SΓςDEF=$\frac{1}{2}$DF•AD=$\frac{1}{4}$BD•EFΘ§ΦΑDE2=BD•EFΘ§Ω…ΒΟDF•AD=$\frac{1}{2}$DF2Θ§Φ¥DF=2ADΘ°
Ϋβ¥π ΫβΘΚΔΌ…ηCF=xΘ§DF=yΘ§BC=hΘ°
ΓΏΥΡ±Ώ–ΈBFDE «Νβ–ΈΘ§
ΓύBF=DF=yΘ§DEΓΈBFΘ°
ΓΏ$\frac{{S}_{ABCD}}{{S}_{BFDE}}$=$\frac{2+\sqrt{3}}{2}$Θ§
Γύ$\frac{Θ®x+yΘ©h}{yh}$=$\frac{2+\sqrt{3}}{2}$Θ§
Γύ$\frac{x}{y}$=$\frac{\sqrt{3}}{2}$Θ§Φ¥cosΓœBFC=$\frac{\sqrt{3}}{2}$Θ§
ΓύΓœBFC=30ΓψΘ§
ÿDEøBFȧ
ΓύΓœEDF=ΓœBFC=30ΓψΘ§
ΓύtanΓœEDF=$\frac{\sqrt{3}}{3}$Θ§
Υυ“‘ΔΌ «’φΟϋΧβΘ°
ΔΎΓΏΥΡ±Ώ–ΈBFDE «Νβ–ΈΘ§
ΓύDF=DEΘ°
ΓΏSΓςDEF=$\frac{1}{2}$DF•AD=$\frac{1}{4}$BD•EFΘ§
”÷ΓΏDE2=BD•EFΘ®“―÷ΣΘ©Θ§
ΓύSΓςDEF=$\frac{1}{4}$DE2=$\frac{1}{4}$DF2Θ§
ΓύDF•AD=$\frac{1}{2}$DF2Θ§
ΓύDF=2ADΘ§
Υυ“‘ΔΎ «’φΟϋΧβΘ°
Ι ―ΓΘΚBΘ°
ΒψΤά ¥ΥΧβΩΦ≤ιΝΥΨΊ–ΈΒΡ–‘÷ ΦΑΝβ–ΈΒΡ–‘÷ Θ§ΫβΧβΒΡΙΊΦϋ «ΔΌœ»«σ≥ωΓœEDFΒΡ”ύœ“Κ· ΐ÷Β»ΖΕ®ΤδΕ» ΐΘ§‘Ό«σ≥ωΤδ’ΐ«–Θ°ΔΎ”ΟΟφΜΐΖ®»ΖΕ®Θ°


 ΩΈ ±―ΒΝΖΫ≠Υ’»ΥΟώ≥ωΑφ…γœΒΝ–¥πΑΗ
ΩΈ ±―ΒΝΖΫ≠Υ’»ΥΟώ≥ωΑφ…γœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° |  | BΘ° |  | CΘ° |  | DΘ° |  |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 4ΘΚ3 | BΘ° | 3ΘΚ4 | CΘ° | 16ΘΚ9 | DΘ° | 9ΘΚ16 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
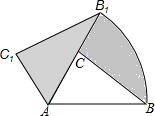 »γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœBAC=50ΓψΘ§AC=2Θ§AB=3Θ°œ÷ΫΪΓςABC»ΤAΒψΡφ ±–ΐΉΣ50ΓψΒΟΒΫΓςAB1C1Θ§‘ρΆΦ÷–ΒΡ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣ$\frac{5}{4}$Π–Θ°
»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœBAC=50ΓψΘ§AC=2Θ§AB=3Θ°œ÷ΫΪΓςABC»ΤAΒψΡφ ±–ΐΉΣ50ΓψΒΟΒΫΓςAB1C1Θ§‘ρΆΦ÷–ΒΡ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣ$\frac{5}{4}$Π–Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
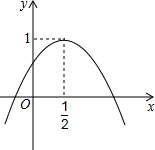 »γΆΦΘ§Εΰ¥ΈΚ· ΐy=ax2+bx+cΒΡΆΦœσ”κy÷α’ΐΑκ÷αœύΫΜΘ§ΤδΕΞΒψΉχ±ξΈΣΘ®$\frac{1}{2}$Θ§1Θ©Θ§œ¬Ν–Ϋα¬έΘΚΔΌabcΘΨ0ΘΜΔΎa=bΘΜΔέa=4c-4ΘΜΔήΖΫ≥Χax2+bx+c=1”–ΝΫΗωœύΒ»ΒΡ Β ΐΗυΘ§Τδ÷–’ΐ»ΖΒΡΫα¬έ «ΔέΔήΘ°Θ®÷ΜΧν–ρΚ≈Φ¥Ω…Θ©Θ°
»γΆΦΘ§Εΰ¥ΈΚ· ΐy=ax2+bx+cΒΡΆΦœσ”κy÷α’ΐΑκ÷αœύΫΜΘ§ΤδΕΞΒψΉχ±ξΈΣΘ®$\frac{1}{2}$Θ§1Θ©Θ§œ¬Ν–Ϋα¬έΘΚΔΌabcΘΨ0ΘΜΔΎa=bΘΜΔέa=4c-4ΘΜΔήΖΫ≥Χax2+bx+c=1”–ΝΫΗωœύΒ»ΒΡ Β ΐΗυΘ§Τδ÷–’ΐ»ΖΒΡΫα¬έ «ΔέΔήΘ°Θ®÷ΜΧν–ρΚ≈Φ¥Ω…Θ©Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
| Ζ÷Ήι | Μ°Φ« | ΤΒ ΐ |
| 25ΓήxΘΦ30 |  | 4 |
| 30ΓήxΘΦ35 | ’ΐ’ΐ’ΐ | 15 |
| 35ΓήxΘΦ40 | ’ΐ’ΐ’ΐ’ΐ’ΐ’ΐ“Μ | 31 |
| 40ΓήxΘΦ45 | ’ΐ“Μ | 6 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com