练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

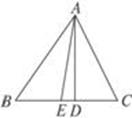
    (1)如图,已知△ABC中,AD⊥BC于D, AE为∠BAC的平分线,∠B=50°,∠C=70°,求∠DAE的度数.

    (2)已知在△ABC中，AD⊥BC于点D，AE平分∠BAC(∠C>∠B).求证：∠DAE=   (∠C－∠B).

     



    （1）10°

    （2）证明：∵AE平分∠BAC(已知)，∴∠EAC=∠BAC(角平分线定义).

    ∵∠BAC+∠B+∠C=180°(三角形三个内角的和等于180°)，

    ∴∠BAC=180°-∠B-∠C(等式性质).

    ∴∠EAC=(180°-∠B-∠C)(等量代换).

    ∵AD⊥BC(已知)，∴∠ADC=90°(垂直定义).

    在△ADC中，∠ADC+∠C+∠DAC=180°(三角形三个内角的和等于180°)，

    ∴∠DAC=180°-∠ADC-∠C(等式性质)=90°-∠C.

    ∴∠EAD=∠EAC-∠DAC=(180°-∠B-∠C)-(90°-∠C)(等量代换)

    =(180°-∠B-∠C)-(180°-2∠C)=(180°-∠B-∠C-180°+2∠C)

    =(∠C-∠B). 

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


     在、、、、、中,分式的个数有（     ）

    A、2个          B、3个            C、4个           D、5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，△ABC中，E、F、D分别是边AB、AC、BC上的点，且满足，则△EFD与△ABC的面积比为　      　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知一次函数的图象经过点A(－3,2)和B(1,6)．则函数的图象与两坐标轴围成的三角形的面积为                                               （  ）

    A、10         B、25             C、12             D、12.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，等边△ABC中，B点在坐标原点，C点坐标为(4,0)，点A关于x轴对称点A′的坐标为__________．

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列四组线段中，可以构成直角三角形的是（　 　）

    A．4，5，6          B．3，4，5        C．2，3，4        D．1，2，3

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在镜子中看到时钟显示的是 ，则实际时间是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


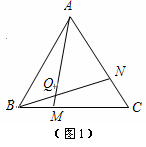
     （1）学完全等三角形以后，老师布置了这样一道题：如图1，点M、N分别在等边△ABC的BC、CA边上，且BM=CN，AM、BN交于点Q．试说明：∠BQM=60°．

    （2）小丽做完后，进行了反思，提出了许多问题，如：

    ①若将题中“BM=CN”与“∠BQM=60°”的位置交换，得到的是否仍是真命题？

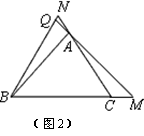
    ②若将题中的点M、N分别移动到BC、CA的延长线上，是否仍能得到∠BQM=60°？

    请你作出判断，在下列横线上填写“是”或“否”：①         ；②       ．

    并对②给出证明．

     


                                                                     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，某海监船向正西方向航行，在A处望见一艘正在作业渔船D在南偏西45°方向，海监船航行到B处时望见渔船D在南偏东45°方向，又航行了半小时到达C处，望见渔船D在南偏东60°方向，若海监船的速度为50海里/小时，则A，B之间的距离为     （取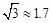 ，结果精确到0.1海里）．

    查看答案和解析>>

    同步练习册答案