Question

3．如图，正方形ABCD的边长为$\sqrt{3}$，点P是边BC所在直线上的一个动点，连接PA，将线段PA绕点P顺时针旋转60°得到线段PF，PF与边CD相交于点E．
（1）当点P在BC边上运动时，
①如图1，当∠BAP=30°，求PE的长；
②如图2，点F与点E重合，求CE的长．
（2）如图3，以点B为坐标原点建立平面直角坐标系，点P在边BC所在直线（即x轴）上运动过程中，点F运动所形成的图象是一条直线，
①求点F运动所形成的直线解析式；
②请直接写出线段BF的最小值．

Answer 1

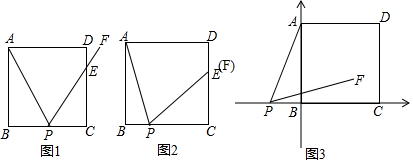
分析 （1）①在Rt△ABP中，求得BP=1，进而得到PC=BC-BP=$\sqrt{3}$-1，在Rt△CPE中，根据∠CEP=90°-∠CPE=30°，PC=$\sqrt{3}$-1，可得PE=2PC=2$\sqrt{3}$-2；
②连接AE，先判定Rt△ABP≌Rt△ADE，得出BP=DE，PC=EC，再设BP=x，在Rt△ABP中，AP²=AB²+BP²=3+x²，在Rt△PCE中，PE²=2PC²=2（$\sqrt{3}$-x）²，根据AP=PE，得出AP²=PE²，进而得到3+x²=2（$\sqrt{3}$-x）²，求得CE=PC=3-$\sqrt{3}$即可；
（2）①点F运动所形成的图象是一条直线，只需求出此直线所经过的两点坐标即可．当点F₁在x轴上时，求得点F₁的坐标为（1，0），当点F₂在y轴上时，求得点F₂的坐标为（0，-$\sqrt{3}$），最后根据待定系数法，求得直线F₁F₂的解析式为y=$\sqrt{3}$x-$\sqrt{3}$；
②在Rt△BF₁F₂中，设点B到F₁F₂的距离为h，则根据$\frac{1}{2}$×BF₁×BF₂=$\frac{1}{2}$×F₁F₂×h，求得h=$\frac{\sqrt{3}}{2}$，根据垂线段最短，即可得到线段BF的最小值．

解答 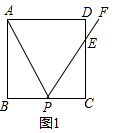解：（1）①如图1，∵四边形ABCD是正方形，
∴AB=BC=AD=$\sqrt{3}$，∠ABC=∠BCD=90°，
在Rt△ABP中，∠BAP=30°，AB=$\sqrt{3}$，
∴∠APB=60°，BP=1，
∴PC=BC-BP=$\sqrt{3}$-1，
∵将线段PA绕点P顺时针旋转60°得到线段PF，
∴∠APF=60°，
∴∠CPE=60°，
在Rt△CPE中，∠CEP=90°-∠CPE=30°，PC=$\sqrt{3}$-1，
∴PE=2PC=2$\sqrt{3}$-2；

②如图2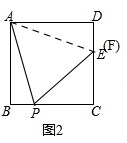，连接AE，
∵点F与点E重合，
∴AP=EP，
∵∠APE=60°，
∴△APE是等边三角形，
∴AP=AE，
在Rt△ABP和Rt△ADE中，
$\left\{\begin{array}{l}{AB=AD}\\{AP=AE}\end{array}\right.$，
∴Rt△ABP≌Rt△ADE（HL），
∴BP=DE，
∴PC=EC，
设BP=x，（0＜x≤$\sqrt{3}$）则PC=DE=$\sqrt{3}$-x，
在Rt△ABP中，AP²=AB²+BP²=3+x²，
在Rt△PCE中，PE²=2PC²=2（$\sqrt{3}$-x）²，
∵AP=PE，
∴AP²=PE²，即：3+x²=2（$\sqrt{3}$-x）²，
∴解得x=2$\sqrt{3}$+3（舍去）或x=2$\sqrt{3}$-3，
∴CE=PC=3-$\sqrt{3}$；

（2）①∵点F运动所形成的图象是一条直线，
∴只需求出此直线所经过的两点坐标即可，
如图3，当点F₁在x轴上时，△P₁AF₁为等边三角形，则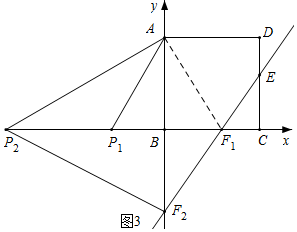
P₁A=P₁F₁=AF₁，∠AP₁E₁=60°，
∵AB⊥P₁F₁，∴P₁B=F₁B，∠ABP₁=90°，
∴∠P₁AB=30°，且AB=$\sqrt{3}$，
由勾股定理得：P₁A=P₁F₁=AF₁=2，
P₁B=F₁B=1，
∴点F₁的坐标为（1，0），
如图3，当点F₂在y轴上时，
∵△P₂AF₂为等边三角形，AB⊥P₂B，
∴AB=F₂B=$\sqrt{3}$，
∴点F₂的坐标为（0，-$\sqrt{3}$），
设直线F₁F₂的解析式为y=kx+b，
则$\left\{\begin{array}{l}{k+b=0}\\{b=-\sqrt{3}}\end{array}\right.$，
解得k=$\sqrt{3}$，
∴直线F₁F₂的解析式为y=$\sqrt{3}$x-$\sqrt{3}$；

②BF的最小值为$\frac{\sqrt{3}}{2}$．
理由：在Rt△BF₁F₂中，设点B到F₁F₂的距离为h，则
$\frac{1}{2}$×BF₁×BF₂=$\frac{1}{2}$×F₁F₂×h，
∴$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{1}{2}$×$\sqrt{{1}^{1}+（\sqrt{3}）^{2}}$×h，
解得h=$\frac{\sqrt{3}}{2}$，
即线段BF的最小值为$\frac{\sqrt{3}}{2}$．

点评 本题属于四边形的综合题，主要考查了正方形的性质，旋转的性质，勾股定理的应用，等边三角形的性质以及待定系数法的运用等，解决问题的关键是作辅助线构造等边三角形以及全等三角形，解题时注意勾股定理、等边三角形三线合一以及方程思想的灵活运用．