
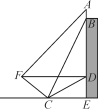
【题目】如图,光明中学一教学楼顶上竖有一块高为AB的宣传牌,点E和点D分别是教学楼底部和外墙上的一点(A,B,D,E在同一直线上),小红同学在距E点9米的C处测得宣传牌底部点B的仰角为67°,同时测得教学楼外墙外点D的仰角为30°,从点C沿坡度为1∶![]() 的斜坡向上走到点F时,DF正好与水平线CE平行.
的斜坡向上走到点F时,DF正好与水平线CE平行.
(1)求点F到直线CE的距离(结果保留根号);
(2)若在点F处测得宣传牌顶部A的仰角为45°,求出宣传牌AB的高度(结果精确到0.01).(注:sin67°≈0.92,tan67°≈2.36,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】(1) 3![]() 米 (2) 1.95米
米 (2) 1.95米
【解析】
(1)利用正切函数定义解三角形求DE长度.(2)利用坡度定义,解直角三角形.
解:(1)过点F作FH⊥CE于H.∵FH∥DE,DF∥HE,∠FHE=90°,∴四边形FHED是矩形,则FH=DE,在Rt△CDE中,DE=CE·tan∠DCE=9×tan30°=3![]() (米),∴FH=DE=3
(米),∴FH=DE=3![]() (米).答:点F到CE的距离为3
(米).答:点F到CE的距离为3![]() 米
米
(2)∵CF的坡度为1∶![]() ,∴在Rt△FCH中,CH=
,∴在Rt△FCH中,CH=![]() FH=9(米),∴EH=DF=18(米),在Rt△BCE中,BE=CE·tan∠BCE=9×tan67°≈21.24(米),∴AB=AD+DE-BE=18+3
FH=9(米),∴EH=DF=18(米),在Rt△BCE中,BE=CE·tan∠BCE=9×tan67°≈21.24(米),∴AB=AD+DE-BE=18+3![]() -21.24≈1.95(米)
-21.24≈1.95(米)
答:宣传牌AB的高度约为1.95米


 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案科目:初中数学 来源: 题型:
【题目】有A、B两组卡片共5张,A组的三张分别写有数字2,4,6,B组的两张分别写有3,5.它们除了数字外没有任何区别,
(1)随机从A组抽取一张,求抽到数字为2的概率;
(2)随机地分别从A组、B组各抽取一张,请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则:若选出的两数之积为3的倍数,则甲获胜;否则乙获胜.请问这样的游戏规则对甲乙双方公平吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
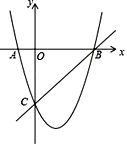
【题目】如图,在平面直角坐标系中,二次函数的图象交坐标轴于A(-1,0),B(4,0),C(0,-4)三点,点P是直线BC下方抛物线上一动点.
(1)写出这个二次函数的解析式;
(2)是否存在点P,使△POC是以OC为底边的等腰三角形?若存在,求出P点坐标;不存在,请说明理由;
(3)过点P作x轴的垂线,交直线BC于点E,动点P运动到什么位置时,线段PE的值最大,求出此时P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步改善路容路貌,提升干线公路美化度,某地相关部门初步拟定派一个工程队对一段长度不少于39000米的公路进行路基标准化整修.该工程队以旧设备与新设备交替使用的方式施工,原计划旧设备每小时整修公路30米,新设备每小时整修公路60米
(1)出于保护旧设备的目的,该工程队计划使用新设备的时间比使用旧设备的时间多![]() ,当这个工程完工时,旧设备的使用时间至少为多少小时?
,当这个工程完工时,旧设备的使用时间至少为多少小时?
(2)通过精确的勘察、测测量、规划,以及新增了部分支线公路整修,此工程的实际施工里程比最初拟定的最少里程39000米多了9000米,于是在实际施工中,旧设备在整修公路效率不变的情况下,使用时间比(1)中的最小值多![]() ,同时,因为工人操作新设备不够熟练,使得得新设备整修公路的效率比原计划下降了
,同时,因为工人操作新设备不够熟练,使得得新设备整修公路的效率比原计划下降了![]() ,使用时间比(1)中新设备使用的最短时间多
,使用时间比(1)中新设备使用的最短时间多![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
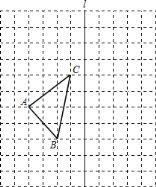
【题目】 如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;(要求A与A1,B与B1,C与C1相对应)
(2)作出△ABC绕点C顺时针方向旋转90°后得到的△A2B2C2;
(3)在(2)的条件下求出线段AC在旋转中所扫过的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
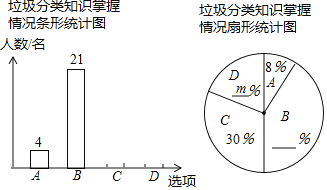
【题目】为响应市政府关于“垃圾不落地![]() 市区更美丽”的主题宣传活动,郑州外国语中学随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解
市区更美丽”的主题宣传活动,郑州外国语中学随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解![]() ”四种,并将调查结果绘制成以下两幅不完整的统计图
”四种,并将调查结果绘制成以下两幅不完整的统计图![]() 请根据图中提供的信息,解答下列问题;
请根据图中提供的信息,解答下列问题;
![]() 求
求![]() ______,并补全条形统计图;
______,并补全条形统计图;
![]() 若我校学生人数为1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有______名;
若我校学生人数为1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有______名;
![]() 已知“非常了解”的是3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请画树状图或列表的方法,求恰好抽到1男1女的概率.
已知“非常了解”的是3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请画树状图或列表的方法,求恰好抽到1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
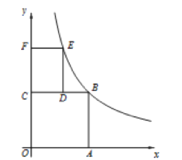
【题目】如图,正方形OABC的边OA,OC在坐标轴上,矩形CDEF的边CD在CB上,且5CD=3CB,边CF在轴上,且CF=2OC-3,反比例函数y=![]() (k>0)的图象经过点B,E,则点E的坐标是____
(k>0)的图象经过点B,E,则点E的坐标是____
查看答案和解析>>
科目:初中数学 来源: 题型:
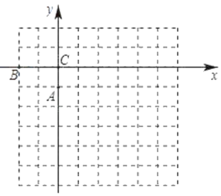
【题目】如图,平面直角坐标系中,以点C为坐标原点,点A(0,﹣1),B(﹣2,0),将△ABC绕点A顺时针旋转90°.
(1)在图中画出旋转后的△AB′C′,并写出点B′、C′的坐标;
(2)已知点D(3,﹣2),在x轴上求作一点P(注:不要求写出P点的坐标),使得PC′+PD的值最小,并求出PC′+PD的最小值;
(3)写出△ABC在旋转过程中,线段AB扫过的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
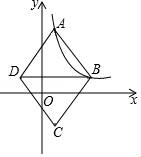
【题目】如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=![]() (k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为
(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com