
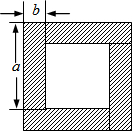
 用四块完全相同的小长方形拼成的一个“回形”正方形.
用四块完全相同的小长方形拼成的一个“回形”正方形.分析 (1)根据阴影部分的面积=4个小长方形的面积=大正方形的面积-小正方形的面积,利用完全平方公式,即可解答;
(2)根据完全平方公式解答;
(3)根据完全平分公式解答.
解答 解:(1)阴影部分的面积为:4ab或(a+b)2-(a-b)2,
得到等式:4ab=(a+b)2-(a-b)2,
说明:(a+b)2-(a-b)2=a2+2ab+b2-(a2-2ab+b2)=a2+2ab+b2-a2+2ab-b2=4ab.
(2)(a-b)2=(a+b)2-4ab=${2}^{2}-4×\frac{3}{4}$=4-3=1,
∴a-b=±1.
(3)根据(1)中的结论,可得:$(x-\frac{1}{x})^{2}=(x+\frac{1}{x})^{2}-4$,
∵x2-3x+1=0,
方程两边都除以x得:$x-3+\frac{1}{x}=0$,
∴$x+\frac{1}{x}=3$,
∴$(x-\frac{1}{x})^{2}=(x+\frac{1}{x})^{2}-4={3}^{2}-4=5$.
点评 本题考查了完全平方公式的几何背景,准确识图,根据阴影部分的面积的两种不同表示方法得到的代数式的值相等列式是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
| 平均数 | 中位数 | 众数 |
| 82.6 | 89.5 | 92 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 印数a(单位:千册) | 1≤a<5 | 5≤a<10 |
| 彩色(单位:元/张) | 2.2 | 2.0 |
| 黑白(单位:元/张) | 0.8 | 0.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\frac{{1-\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
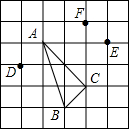 在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )
在边长为1的正方形网格中标有A、B、C、D、E、F六个格点,根据图中标示的各点位置,与△ABC全等的是( )| A. | △ACF | B. | △ACE | C. | △ABD | D. | △CEF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )
如图,已知直线y=x+2与双曲线y=$\frac{m-3}{x}$在第二象限有两个交点,则实数m的取值范围为( )| A. | m>2 | B. | m>2且m≠3 | C. | 2<m≤3 | D. | 2<m<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com