练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．在数0.$\stackrel{•}{3}$1$\stackrel{•}{3}$，$\sqrt{2}$，π，$\frac{22}{7}$，-0.101101110…（每2个0之间多一个1）中，无理数的个数有（　　）
    A．1个B．2个C．3个D．4个

    分析 根据无理数、有理数的定义即可判定选择项．

    解答 解：$\sqrt{2}$，π，-0.101101110…（每2个0之间多一个1）是无理数，
    故选：C．

    点评 此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，$\sqrt{6}$，0.8080080008…（每两个8之间依次多1个0）等形式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．如图，直线y=-x+3与x轴，y轴分别相交于点B，C，经过B，C两点的抛物线y=ax2+bx+c与x轴的另一交点为A，顶点为P，且对称轴是直线x=2．
    （1）求该抛物线的函数表达式；
    （2）请问在抛物线上是否存在点Q，使得以点B，C，Q为顶点的三角形为直角三角形？若存在，请求出点Q的坐标；若不存在，请说明理由；
    （3）过S（0，4）的动直线l交抛物线于M，N两点，试问抛物线上是否存在定点T，使得不过定点T的任意直线l都有∠MTN=90°？若存在，请求出点T的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

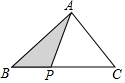    12．如图，已知△ABC中，点P从点B出发，沿BC向终点C运动，当到达点C时停止运动，设PB=x，则△PAB（图中阴影部分）的面积S与x之间的关系用图可以表示为（　　）
    A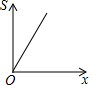．B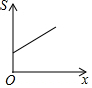．C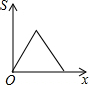．D．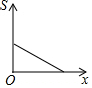

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．先化简（$\frac{1}{n}$+1）+$\frac{{n}^{2}-1}{{n}^{2}-2n+1}$，并从0、-1、$\frac{1}{2}$中选一个你认为合适的数作为n的值，代入求值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．如图，使用圆规和直尺分别画出∠AOB和∠BOC的角平分线OM和ON，如果∠MON=68°，那么：
    （1）在图中作出角平分线OM、ON；
    （2）写出∠AOC的度数136°．
    （3）反向延长AO到D，写出与∠DOM互补的角：∠AOM，∠BOM．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    6．下列方程中，是无理方程的为（　　）
    A．$\sqrt{2}x$+1=$\sqrt{3}$B．$\sqrt{2-x}$+x=0C．$\frac{\sqrt{2}}{x}+1=\sqrt{3}$D．$\frac{x}{\sqrt{2}}+1=\sqrt{3}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．解下列各方程
    （1）2（x-5）+3x=5         
    （2）$\frac{2x+1}{3}$-$\frac{4x-3}{2}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．多项式：①16x2-8x；②（x-1）2-4（x-1）2；③（x+1）4-4（x+1）2+4x2；④-4x2-1+4x分解因式后，结果中含有相同因式的是（　　）
    A．①和②B．③和④C．①和④D．②和③

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知a：b=5：6，b：c=$\frac{3}{10}$：0.5，求a：b：c．

    查看答案和解析>>

    同步练习册答案