Question

18．如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD．
（1）求证：四边形OCED是菱形；
（2）若AD=2CD，菱形的面积是16，求AC的长．

Answer 1

分析 （1）根据对边平行得四边形OCED是平行四边形，由原矩形对角线相等且互相平分得OC=OD，所以四边形OCED是菱形；
（2）连接对角线，根据菱形对角线平分面积得出△OCD的面积是菱形面积的一半=8，设CD=x，根据中位线性质求出OF的长，根据三角形面积公式列方程解出即可．

解答 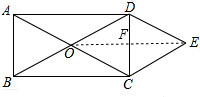证明：（1）∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形，
∵四边形ABCD是矩形，
∴AC=BD，OD=$\frac{1}{2}$BD，OC=$\frac{1}{2}$AC，
∴OC=OD，
∴?OCED是菱形；
（2）∵S_菱形=16，
∴S_△OCD=8，
连接OE，交CD于F，则OE⊥CD，
设CD=x，则AD=2x，
∵AO=OC，DF=FC，
∴OF=$\frac{1}{2}$AD=x，
∴S_△OCD=$\frac{1}{2}$CD•OF=$\frac{1}{2}{x}^{2}$=8
x=±4，
∵x＞0，
∴x=4，
∴AC=$\sqrt{A{D}^{2}+D{C}^{2}}$=$\sqrt{（2x）^{2}+{x}^{2}}$=$\sqrt{5}$x=4$\sqrt{5}$．

点评 本题既考查了菱形的性质，也考查了矩形的性质，是常考题型，难度不大；需要熟练掌握矩形、菱形的边、角、对角线的关系，不能互相混淆．