
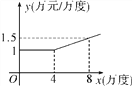
【题目】某工厂在生产过程中每消耗1万度电可以产生产值5.5万元,电力公司规定,该工厂每月用电量不得超过16万度;月用电量不超过4万度时,单价都是1万元/万度;超过4万度时,超过部分电量单价将按用电量进行调整.电价y与月用电量x的函数关系可以用下图来表示(效益=产值-用电量×电价).
(1)求y与月用电量x之间的函数关系式,并写出自变量的取值范围;
(2)设工厂的月效益为z(万元),写出z与用电量x之间的函数关系式;
(3)求工厂最大月效益.
【答案】(1);(2) z= ;(3)工厂最大月效益为54万元.
;(3)工厂最大月效益为54万元.
【解析】分析:(1)根据题意,电价y与用电量x的函数关系式是分段函数,当0≤x≤4时y=1,当4<x≤16时待定系数法可求得,(2)根据效益=产值-用电量×电价,分0≤x≤4,4<x≤16两种情况分别表示可得,(3)根据一次函数和二次函数性质结合自变量取值范围得到最大值,比较即可.
详解:(1)由题图知电价y与用电量x的函数关系式是分段函数.
当0≤x≤4时,y=1,
当4<x≤16时,函数是过点(4,1)和(8,1.5)的一次函数,
设一次函数为y=kx+b,
∴![]() ,
,
解得![]() ,
,
∴电价y与用电量x的函数关系为
y= ,
,
(2)月效益z与用电量x之间的函数关系式为:
z= ,
,
即z= ,
,
(3)当0≤x≤4时,z=![]() x,此时,z随着x的增大而增大,
x,此时,z随着x的增大而增大,
∴当x=4时,z取最大值为18.
当4<x≤16时,z=-![]() x2+
x2+![]() x-2=-
x-2=-![]() (x-22)2+
(x-22)2+![]() ,
,
∴当x≤22时,z随x的增大而增大,
∴当x=16时,z取最大值为54.
故当0≤x≤16时,z的最大值为54,
即工厂最大月效益为54万元.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
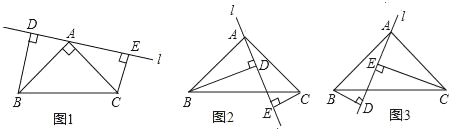
【题目】在△ABC中,∠BAC=90°,AB=AC,l是过A的一条直线,BD⊥AE于D,CE⊥AE于E.求证:
(1)当直线l绕点A旋转到如图1位置时,试说明:DE=BD+CE.
(2)若直线l绕点A旋转到如图2位置时,试说明:DE=BD﹣CE.
(3)若直线l绕点A旋转到如图3位置时,试问:BD与DE,CE具有怎样的等量关系?请写出结果,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣ ![]() x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣
x+4交x轴于点A,交y轴于点C,抛物线y=ax2﹣ ![]() x+c过点A,交y轴于点B(0,﹣2)
x+c过点A,交y轴于点B(0,﹣2)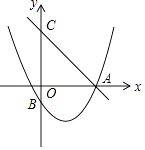
(1)求抛物线的解析式;
(2)点M为抛物线在第四象限部分上的一个动点,求四边形BMAC面积的最大值;
(3)点D为抛物线对称轴上一点,规定:d=|AD﹣BD|,探究d是否存在最大值?若存在,请直接写出d的最大值及此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
![]()
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点(0,﹣3),且顶点坐标为(﹣1,﹣4).
(1)求该二次函数的解析式;
(2)设该二次函数的图象与x轴的交点为A、B,与y轴的交点为C,求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上三点A,O,B对应的数分别为﹣5,0,1,点M为数轴上任意一点,其对应的数为x.
请回答问题:
![]()
(1)A、B两点间的距离是_____,若点M到点A、点B的距离相等,那么x的值是_____;
(2)若点A先沿着数轴向右移动6个单位长度,再向左移动4个单位长度后所对应的数字是 ____ ;
(3)当x为何值时,点M到点A、点B的距离之和是8;
(4)如果点M以每秒3个单位长度的速度从点O向左运动时,点A和点B分别以每秒1个单位长度和每秒4个单位长度的速度也向左运动,且三点同时出发,那么几秒种后点M运动到点A、点B之间,且点M到点A、点B的距离相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的面积是60,请完成下列问题:
(1)如图①,若AD是△ABC的BC边上的中线,则△ABD的面积 _△ACD的面积(选填“>”“<”或“=”).
(2)如图②,若CD,BE分别是△ABC的AB,AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO,同理:S△CEO=S△AEO,设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y,由题意得:S△ABE=![]() S△ABC=30,S△ADC=
S△ABC=30,S△ADC=![]() S△ABC=30,可列方程组为: ,通过解这个方程组可得四边形ADOE的面积为 .
S△ABC=30,可列方程组为: ,通过解这个方程组可得四边形ADOE的面积为 .
(3)如图③,AD∶DB=1∶3,CE∶AE=1∶2,请你计算四边形ADOE的面积,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界读书日,新华书店矩形购书优惠活动:①一次性购书不超过100元,不享受打折优惠;②一次性购书超过100元但不超过200元一律八折;③一次性购书200元以上一律打六折.小丽在这次活动中,两次购书总共付款190.4元,第二次购书原价是第一次购书原价的3倍,那么小丽这两次购书原价的总和是_____元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com