
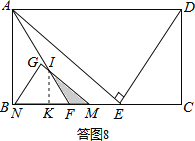
”¾ĢāÄæ”æŅŃÖŖ£ŗŌŚ¾ŲŠĪABCDÖŠ£¬EĪŖ±ßBCÉĻµÄŅ»µć£¬AE”ĶDE£¬AB=12£¬BE=16£¬FĪŖĻ߶ĪBEÉĻŅ»µć£¬EF=7£¬Į¬½ÓAF£®ČēĶ¼1£¬ĻÖÓŠŅ»ÕÅÓ²Ö½Ę¬”÷GMN£¬”ĻNGM=900£¬NG=6£¬MG=8£¬Š±±ßMNÓė±ßBCŌŚĶ¬Ņ»Ö±ĻßÉĻ£¬µćNÓėµćEÖŲŗĻ£¬µćGŌŚĻ߶ĪDEÉĻ£®ČēĶ¼2£¬”÷GMN“ÓĶ¼1µÄĪ»ÖĆ³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲEBĻņµćBŌČĖŁŅĘ¶Æ£¬Ķ¬Ź±£¬µćP“ÓAµć³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲADĻņµćDŌČĖŁŅĘ¶Æ£¬µćQĪŖÖ±ĻßGNÓėĻ߶ĪAEµÄ½»µć£¬Į¬½ÓPQ£®µ±µćNµ½“ļÖÕµćBŹ±£¬”÷GMNPŗĶµćĶ¬Ź±Ķ£Ö¹ŌĖ¶Æ£®ÉčŌĖ¶ÆŹ±¼äĪŖtĆė£¬½ā“šĪŹĢā£ŗ

£Ø1£©ŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬µ±µćGŌŚĻ߶ĪAEÉĻŹ±£¬ĒótµÄÖµ£»
£Ø2£©ŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬ŹĒ·ń“ęŌŚµćP£¬Ź¹”÷APQŹĒµČŃüČż½ĒŠĪ£¬Čō“ęŌŚ£¬Ēó³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£»
£Ø3£©ŌŚÕūøöŌĖ¶Æ¹ż³ĢÖŠ£¬Éč”÷GMNÓė”÷AEFÖŲµž²æ·ÖµÄĆ껿ĪŖS£¬ĒėÖ±½ÓŠ“³öSÓėtµÄŗÆŹż¹ŲĻµŹ½ŅŌ¼°×Ō±äĮætµÄȔֵ·¶Ī§£®
”¾“š°ø”æ£Ø1£©t=10Ćė£»£Ø2£©“ęŌŚ£¬t=![]() £¬
£¬![]() »ņ
»ņ![]() Ćė£»£Ø3£©
Ćė£»£Ø3£©![]() £»
£»![]() £»
£»![]() £»
£»![]() £®
£®
”¾½āĪö”æ
£Ø1£©Óɹ“¹É¶ØĄķ£¬Ēó³öMNµÄ³¤£¬µćQŌĖ¶Æµ½AEÉĻŹ±µÄ¾ąĄėMNµÄ³¤£¬Ąė“Ó¶ų³żŅŌĖŁ¶Č¼“µĆtµÄÖµ£»
£Ø2£©”÷APQŹĒµČŃüČż½ĒŠĪ£¬·ÖĪŖČżÖÖĒéŠĪ£¬ŠčŅŖ·ÖĄąĢÖĀŪ£¬±ÜĆāĀ©½ā£®Čē“šĶ¼2”¢“šĶ¼3”¢“šĶ¼4ĖłŹ¾£»
£Ø3£©ÕūøöŌĖ¶Æ¹ż³Ģ·ÖĪŖĖÄøö½×¶Ī£¬Ćæøö½×¶ĪÖŲµžĶ¼ŠĪµÄŠĪדø÷²»ĻąĶ¬£¬Čē“šĶ¼5-“šĶ¼8ĖłŹ¾£¬·Ö±šĒó³öĘäĆ껿µÄ±ķ“ļŹ½£®
½ā£ŗ£Ø1£©”ß”ĻNGM=900£¬NG=6£¬MG=8£¬£¬
”ąÓɹ“¹É¶ØĄķ£¬µĆNM=10£®
µ±µćGŌŚĻ߶ĪAEÉĻŹ±£¬ČēĶ¼£¬
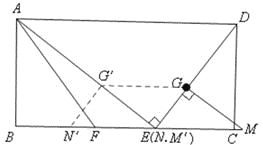
“ĖŹ±£¬GG”ä=MN=10£®
”ß”÷GMN“ÓĶ¼1µÄĪ»ÖĆ³ö·¢£¬ŅŌĆæĆė1øöµ„Ī»µÄĖŁ¶ČŃŲEBĻņµćBŌČĖŁŅĘ¶Æ£¬
”ąt=10Ćė£®
£Ø2£©“ęŌŚ·ūŗĻĢõ¼žµÄµćP£®
ŌŚRt”÷ABEÖŠ£¬AB=12£¬BE=16£¬Óɹ“¹É¶ØĄķµĆ£ŗAE=20£®
Éč”ĻAEB=¦Č£¬Ōņsin¦Č=![]() £¬cos¦Č=
£¬cos¦Č=![]() £®
£®
”ßNE=t£¬”ąQE=NEcos¦Č=![]() t£¬AQ=AE-QE=20-
t£¬AQ=AE-QE=20-![]() t£®
t£®
”÷APQŹĒµČŃüČż½ĒŠĪ£¬ÓŠČżÖÖæÉÄܵÄĒéŠĪ£ŗ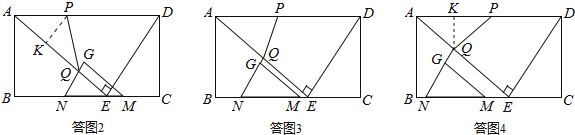
¢ŁAP=PQ£®Čē“šĶ¼2ĖłŹ¾£ŗ
¹żµćP×÷PK”ĶAEÓŚµćK£¬ŌņAK=APcos¦Č=![]() t£®
t£®
”ßAQ=2AK£¬”ą20-![]() t=2”Į
t=2”Į![]() t£¬
t£¬
½āµĆ£ŗt=![]() £»
£»
¢ŚAP=AQ£®Čē“šĶ¼3ĖłŹ¾£ŗ
ÓŠt=20-![]() t£¬
t£¬
½āµĆ£ŗt=![]() £»
£»
¢ŪAQ=PQ£®Čē“šĶ¼4ĖłŹ¾£ŗ
¹żµćQ×÷QK”ĶAPÓŚµćK£¬ŌņAK=AQcos¦Č=£Ø20-![]() t£©”Į
t£©”Į![]() =16-
=16-![]() t£®
t£®
”ßAP=2AK£¬”ąt=2£Ø16-![]() t£©£¬
t£©£¬
½āµĆ£ŗt=![]() £®
£®
×ŪÉĻĖłŹö£¬µ±t=![]() £¬
£¬![]() »ņ
»ņ![]() ĆėŹ±£¬“ęŌŚµćP£¬Ź¹”÷APQŹĒµČŃüČż½ĒŠĪ£®
ĆėŹ±£¬“ęŌŚµćP£¬Ź¹”÷APQŹĒµČŃüČż½ĒŠĪ£®
ÓɾŲŠĪABCDÖŠ£¬AB=12£¬BE=16£¬µĆAE=20£®
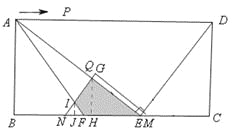
¢Łµ±0£¼t”Ü10Ź±£¬Ļ߶ĪGNÓėĻ߶ĪAEĻą½»£¬ČēĶ¼£¬¹żµćQ×÷QH”ĶBCÓŚµćH£¬QI”ĶABÓŚµćI£¬¹żµćP×÷PJ”ĶIJÓŚµćJ£®
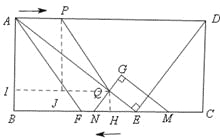
øł¾ŻĢāŅā£¬ÖŖAP=EN=t£¬
ÓÉ”÷QNE”×”÷GNMµĆ![]() £¬¼“
£¬¼“![]()
”ą![]() £¬”ą
£¬”ą![]() £®
£®
ÓÉ”÷QHE”×”÷NGMµĆ![]() £¬¼“
£¬¼“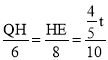 £¬
£¬
”ą![]()
”ą![]() £®
£®
”ą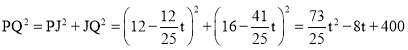 £®
£®
ČōAP=AQ£¬Ōņ![]() £¬½āµĆ
£¬½āµĆ![]() £¬²»“ęŌŚ£»
£¬²»“ęŌŚ£»
ČōAP=PQ£¬Ōņ![]() £¬
£¬
”ą![]() ”÷£¼0£¬ĪŽ½ā£¬²»“ęŌŚ£»
”÷£¼0£¬ĪŽ½ā£¬²»“ęŌŚ£»
ČōAQ=PQ£¬Ōņ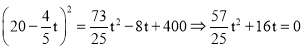 £¬ĪŽÕżŹż½ā£¬²»“ęŌŚ£®
£¬ĪŽÕżŹż½ā£¬²»“ęŌŚ£®
¢Śµ±10£¼t”Ü16Ź±£¬Ļ߶ĪGNµÄŃÓ³¤ĻßÓėĻ߶ĪAEĻą½»£¬ČēĶ¼£¬¹żµćQ×÷QH”ĶBCÓŚµćH£¬QI”ĶABÓŚµćI£¬¹żµćP×÷PJ”ĶIJÓŚµćJ£®
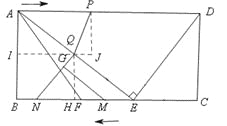
Ķ¬ÉĻ£¬AP=EN=t£¬
ÓÉ”÷QNE”×”÷GNMµĆ![]() £¬¼“
£¬¼“![]() £¬
£¬
”ą![]() ”ą
”ą![]() £®
£®
ÓÉ”÷QHE”×”÷NGMµĆ![]() £¬¼“
£¬¼“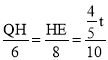 £¬
£¬
”ą![]()
”ą![]() £®
£®
”ą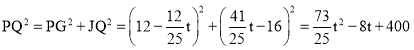 £®
£®
ČōAP=AQ£¬Ōņ![]() £¬½āµĆ
£¬½āµĆ![]() £®
£®
ČōAP=PQ£¬Ōņ![]() £¬
£¬
”ą![]() ”÷£¼0£¬ĪŽ½ā£¬²»“ęŌŚ£»
”÷£¼0£¬ĪŽ½ā£¬²»“ęŌŚ£»
ČōAQ=PQ£¬Ōņ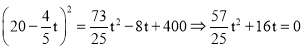 £¬ĪŽÕżŹż½ā£¬²»“ęŌŚ£®
£¬ĪŽÕżŹż½ā£¬²»“ęŌŚ£®
×ŪÉĻĖłŹö£¬“ęŌŚ![]() £¬Ź¹”÷APQŹĒµČŃüČż½ĒŠĪ£®
£¬Ź¹”÷APQŹĒµČŃüČż½ĒŠĪ£®
£Ø3£©µ±0£¼t”Ü7Ź±£¬”÷GMNÓė”÷AEFÖŲµž²æ·ÖµÄĆ껿µČÓŚ”÷QNEµÄĆ껿£¬
ÓÉ£Ø2£©¢Ł£¬EN=t£¬![]() £¬”ą
£¬”ą![]() £®
£®
µ±7£¼t”Ü10Ź±£¬ČēĶ¼£¬”÷GMNÓė”÷AEFÖŲµž²æ·ÖµÄĆ껿µČÓŚĖıߊĪQIFEµÄĆ껿£¬ĖüµČÓŚ”÷NQEµÄĆ껿¼õČ„”÷NIFµÄĆ껿£®
ÓÉ£Ø2£©¢Ł£¬EN=t£¬![]() £¬”ą
£¬”ą![]() £®
£®
¹żµćI ×÷IJ”ĶBCÓŚµćJ£¬
”ßEF=7£¬EN=t£¬”ą![]() £®
£®
ÓÉ”÷FJI”×”÷FBAµĆ![]() £¬¼“
£¬¼“![]() £®
£®
ÓÉ”÷INJ”×”÷MNGµĆ![]() £¬¼“
£¬¼“![]() £®
£®
¶žŹ½Ļą¼Ó£¬µĆ![]() £®”ą
£®”ą![]()
”ą![]() £®
£®
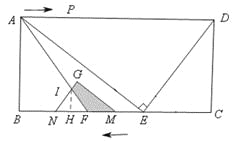
µ±10£¼t”Ü![]() Ź±£¬ČēĶ¼£¬”÷GMNÓė”÷AEFÖŲµž²æ·ÖµÄĆ껿µČÓŚĖıߊĪGIFMµÄĆ껿£¬ĖüµČÓŚ”÷GMNµÄĆ껿¼õČ„”÷INFµÄĆ껿£®
Ź±£¬ČēĶ¼£¬”÷GMNÓė”÷AEFÖŲµž²æ·ÖµÄĆ껿µČÓŚĖıߊĪGIFMµÄĆ껿£¬ĖüµČÓŚ”÷GMNµÄĆ껿¼õČ„”÷INFµÄĆ껿£®
¹żµćI ×÷IH”ĶBCÓŚµćH£¬
”ßEF=7£¬EN=t£¬”ą![]() £®
£®
ÓÉ”÷FHG”×”÷FBAµĆ![]() £¬¼“
£¬¼“![]() £®
£®
ÓÉ”÷INH”×”÷MNGµĆ![]() £¬¼“
£¬¼“![]() £®
£®
¶žŹ½Ļą¼Ó£¬µĆ![]() £®”ą
£®”ą![]() £®
£®
”ą![]() £®
£®
¢Üµ±![]() £¼t”Ü16Ź±Ź±£¬Čē“šĶ¼8ĖłŹ¾£ŗ
£¼t”Ü16Ź±Ź±£¬Čē“šĶ¼8ĖłŹ¾£ŗ
FM=FE-ME=FE-£ØNE-MN£©=17-t£®
ÉčGMÓėAF½»ÓŚµćI£¬¹żµćI×÷IK”ĶMNÓŚµćK£®
”ßtan”ĻIFK=![]() =
=![]() £¬”ąæÉÉčIK=4x£¬FK=3x£¬ŌņKM=3x+17-t£®
£¬”ąæÉÉčIK=4x£¬FK=3x£¬ŌņKM=3x+17-t£®
”ßtan”ĻIMF=![]()
![]() =
=![]() £¬
£¬
½āµĆ£ŗx=![]() £Ø17-t£©£®
£Ø17-t£©£®
”ąIK=4x=![]() £Ø17-t£©£®
£Ø17-t£©£®
”ąS=![]() FMIK=
FMIK=![]() £Øt-17£©2£®
£Øt-17£©2£®
×ŪÉĻĖłŹö£¬SÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½ĪŖ£ŗ![]() £»
£»![]() £»
£»![]() £»
£»![]() £®
£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶ž“ĪŗÆŹży=ax2+2ax+3a2+3£ØĘäÖŠxŹĒ×Ō±äĮ棩£¬µ±x”Ż2Ź±£¬yĖęxµÄŌö“ó¶ųŌö“ó£¬ĒŅ-2”Üx”Ü1Ź±£¬yµÄ×ī“óÖµĪŖ9£¬ŌņaµÄÖµĪŖ![]() ””””
””””![]()
A. 1»ņ![]() B. -
B. -![]() »ņ
»ņ![]() C.
C. ![]() D. 1
D. 1
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĘū³µ¼ŻŹ»Ō±×ųŌŚ¼ŻŹ»×łĪ»ÉĻ£¬ĘäŹÓĻß¹Ū²ģ²»µ½µÄµŲ·½½Š”°Ęū³µĆ¤Ēų”±£®ČēĶ¼ŹĒŅ»Į¾Ęū³µµÄ”°³µĶ·Ć¤Ēų”±Ź¾ŅāĶ¼£¬ĘäÖŠAC”ĶBC£¬DE”ĶBC£¬¼ŻŹ»Ō±Ėł“¦Ī»ÖƵÄø߶ČACĪŖ1.4Ć×£¬¼ŻŹ»Ō±×łĪ»ACÓė³µĶ·DEÖ®¼ä¾ąĄėĪŖ2Ć×£¬µ±¼ŻŹ»Ō±“ÓAµć¹Ū²ģ³µĶ·DµćŹ±£¬ĘäŹÓĻßµÄø©½ĒĪŖ12”ć£¬µćA”¢D”¢BŌŚĶ¬Ņ»Ö±ĻßÉĻ£®
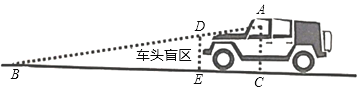
£Ø1£©ĒėÖ±½ÓŠ“³ö”ĻABCµÄ¶ČŹż£»
£Ø2£©Ēó”°³µĶ·Ć¤Ēų”±µćB”¢EÖ®¼äµÄ¾ąĄė£®£Ø½į¹ū¾«Č·µ½0.1Ć×£©²Īæ¼Źż¾Ż£ŗsin12”ć£½0.20£¬cas12”ć£½0.99£¬tan12”ć£½0.21
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ė®æā“ó°ÓµÄŗį¶ĻĆęĪŖĖıߊĪABCD£¬ĘäÖŠAD”ĪBC£¬°Ó¶„BC=10Ć×£¬°Óøß20Ć×£¬Š±ĘĀABµÄĘĀ¶Či=1£ŗ2.5£¬Š±ĘĀCDµÄĘĀ½ĒĪŖ30”ć£®
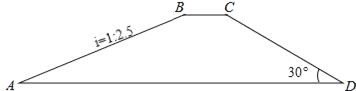
£Ø1£©Ēó°Óµ×ADµÄ³¤¶Č£Ø½į¹ū¾«Č·µ½1Ć×£©£»
£Ø2£©Čō°Ó³¤100Ć×£¬Ēó½ØÖžÕāøö“ó°ÓŠčŅŖµÄĶĮŹÆĮĻ£Ø²Īæ¼Źż¾Ż£ŗ ![]() £©
£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
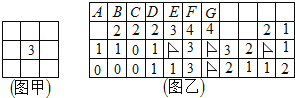
”¾ĢāÄæ”æµēÄŌĻµĶ³ÖŠÓŠøö”°ÉØĄ×”±ÓĪĻ·£¬ŅŖĒóÓĪĻ·Õß±ź³öĖłÓŠµÄĄ×£¬ÓĪĻ·¹ęŌņ£ŗŅ»øö·½æéĻĀĆę×ī¶ąĀńŅ»øöĄ×£¬Čē¹ūĪŽĄ×£¬ĻĘæŖ·½æéĻĀĆę¾Ķ±źÓŠŹż×Ö£¬ĢįŠŃÓĪĻ·Õß“ĖŹż×ÖÖÜĪ§µÄ·½æé£Ø×ī¶ą°Ėøö£©ÖŠĄ×µÄøöŹż£ØŹµ¼ŹÓĪĻ·ÖŠ£¬0Ķس£Ź”ĀŌ²»±ź£¬ĪŖ·½±ć“ó¼ŅŹ¶±šÓėÓ”Ė¢£¬ĪŅ°ŃĶ¼ŅŅÖŠµÄ0¶¼±ź³öĄ“ĮĖ£¬ŅŌŹ¾ÓėĪ“ĻĘæŖÕßµÄĒų±š£©£¬ČēĶ¼¼×ÖŠµÄ”°3”±±ķŹ¾ĖüµÄÖÜĪ§°Ėøö·½æéÖŠ½öÓŠ3øöĀńÓŠĄ×£®Ķ¼ŅŅŹĒÕÅČżĶęÓĪĻ·ÖŠµÄ¾Ö²æ£¬Ķ¼ÖŠÓŠ4øö·½æé¼ŗČ·¶ØŹĒĄ×£Ø·½æéÉĻ±źÓŠĘģ×Ó£©£¬ŌņĶ¼ŅŅµŚŅ»ŠŠ“Ó×óŹżĘšµÄĘßøö·½æéÖŠ£Ø·½æéÉĻ±źÓŠ×ÖÄø£©£¬Äܹ»Č·¶ØŅ»¶ØŹĒĄ×µÄÓŠ
”” ””£®£ØĒėĢīČė·½æéÉĻµÄ×ÖÄø£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ![]() ”¢
”¢![]() Į½µŲĻą¾ą30Ē§Ć×£¬ŅŃÖŖ¼×”¢ŅŅĮ½ČĖ·Ö±šĘļ×ŌŠŠ³µŗĶĦĶŠ³µ“Ó
Į½µŲĻą¾ą30Ē§Ć×£¬ŅŃÖŖ¼×”¢ŅŅĮ½ČĖ·Ö±šĘļ×ŌŠŠ³µŗĶĦĶŠ³µ“Ó![]() µŲ³ö·¢Ē°Ķł
µŲ³ö·¢Ē°Ķł![]() µŲ£¬Ķ¾ÖŠŅŅŅņŠŽ³µµ¢ĪóĮĖŠ©Ź±¼ä£¬Č»ŗóÓÖ¼ĢŠųøĻĀ·.Ķ¼5ÖŠµÄĻ߶Ī
µŲ£¬Ķ¾ÖŠŅŅŅņŠŽ³µµ¢ĪóĮĖŠ©Ź±¼ä£¬Č»ŗóÓÖ¼ĢŠųøĻĀ·.Ķ¼5ÖŠµÄĻ߶Ī![]() ŗĶÕŪĻß
ŗĶÕŪĻß![]() ·Ö±š·“Ó³ĮĖ¼×”¢ŅŅĮ½ČĖĖłŠŠµÄĀ·³Ģ
·Ö±š·“Ó³ĮĖ¼×”¢ŅŅĮ½ČĖĖłŠŠµÄĀ·³Ģ![]() £ØĒ§Ć×£©ÓėŹ±¼ä
£ØĒ§Ć×£©ÓėŹ±¼ä![]() £Ø·Ö£©µÄŗÆŹż¹ŲĻµ£¬øł¾ŻĶ¼ĻńĢį¹©µÄŠÅĻ¢»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø·Ö£©µÄŗÆŹż¹ŲĻµ£¬øł¾ŻĶ¼ĻńĢį¹©µÄŠÅĻ¢»Ų“šĻĀĮŠĪŹĢā£ŗ
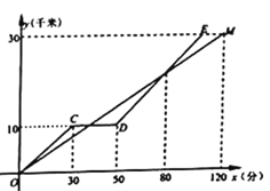
£Ø1£©¼×Ęļ×ŌŠŠ³µµÄĖŁ¶ČŹĒ_________Ē§Ć×/·ÖÖÓ£»
£Ø2£©Į½ČĖµŚ¶ž“ĪĻąÓöŹ±¾ąĄė![]() µŲ________Ē§Ć×£»
µŲ________Ē§Ć×£»
£Ø3£©Ļ߶Ī![]() ·“Ó³ĮĖŅŅŠŽŗĆ³µŗóĖłŠŠµÄĀ·³Ģ
·“Ó³ĮĖŅŅŠŽŗĆ³µŗóĖłŠŠµÄĀ·³Ģ![]() £ØĒ§Ć×£©ÓėŹ±¼ä
£ØĒ§Ć×£©ÓėŹ±¼ä![]() £Ø·Ö£©µÄŗÆŹż¹ŲĻµ.ĒėĒó³öĻ߶Ī
£Ø·Ö£©µÄŗÆŹż¹ŲĻµ.ĒėĒó³öĻ߶Ī![]() µÄ±ķ“ļŹ½¼°Ęä¶ØŅåÓņ.
µÄ±ķ“ļŹ½¼°Ęä¶ØŅåÓņ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
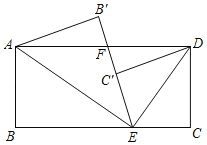
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŌŚ¾ŲŠĪABCDÖŠ£¬AB£½1£¬ŌŚĻ߶ĪBCÉĻČ”Ņ»µćE£¬Į¬½ÓAE”¢ED£¬½«”÷ABEŃŲAE·ÕŪ£¬Ź¹µćBĀäŌŚB'“¦£¬Ļ߶ĪEB'½»ADÓŚµćF£®½«”÷ECDŃŲDE·ÕŪ£¬Ź¹µćCµÄ¶ŌÓ¦µćC'ĀäŌŚĻ߶ĪEB'ÉĻ£¬ĒŅµćC'Ē”ŗĆĪŖEB'µÄÖŠµć£¬ŌņĻ߶ĪEFµÄ³¤ĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬±ß³¤ĪŖ8µÄÕż·½ŠĪOABCµÄĮ½±ßŌŚ×ų±źÖįÉĻ£¬ŅŌµćCĪŖ¶„µćµÄÅ×ĪļĻß¾¹żµćA£¬µćPŹĒÅ×ĪļĻßÉĻµćA£¬C¼äµÄŅ»øö¶Æµć£Øŗ¬¶Ėµć£©£¬¹żµćP×÷PF”ĶBCÓŚµćF£¬µćD£¬EµÄ×ų±ź·Ö±šĪŖ£Ø0£¬6£©£¬£Ø©4£¬0£©£¬Į¬½ÓPD£¬PE£¬DE£®
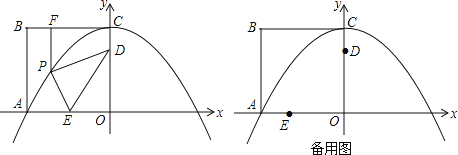
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©Čōd£½|PD©PF|£®ĒėĖµĆ÷dŹĒ·ńĪŖ¶ØÖµ£æČōŹĒ¶ØÖµ£¬ĒėĒó³öĘä“󊔣»Čō²»ŹĒ¶ØÖµ£¬ĒėĖµĆ÷Ęä±ä»Æ¹ęĀÉ£æ
£Ø3£©Ēó³ö”÷PDEÖܳ¤Č”Öµ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¼×ŅŅĮ½³µ·Ö±š“ÓA”¢BĮ½µŲ³ö·¢£¬ĻąĻņŌČĖŁŠŠŹ»£¬ŅŃÖŖŅŅ³µĻČ³ö·¢£¬1Š”Ź±ŗó¼×³µŌŁ³ö·¢£®Ņ»¶ĪŹ±¼äŗ󣬼×ŅŅĮ½³µŌŚŠŻĻ¢Õ¾CµŲĻąÓö£ŗµ½“ļCµŲŗó£¬ŅŅ³µ²»ŠŻĻ¢¼ĢŠų°“ŌĖŁĒ°ĶłAµŲ£¬¼×³µŠŻĻ¢°ėŠ”Ź±ŗóŌŁ°“ŌĖŁĒ°ĶłBµŲ£¬¼×³µµ½“ļBµŲĶ£Ö¹ŌĖ¶Æ£»ŅŅ³µµ½AµŲŗóĮ¢æĢŌĖŁ·µ»ŲBµŲ£¬ŅŃÖŖĮ½³µ¼äµÄ¾ąĄėy£Økm£©ĖęŅŅ³µŌĖ¶ÆµÄŹ±¼äx£Øh£©±ä»ÆČēĶ¼£¬Ōņµ±¼×³µµ½“ļBµŲŹ±£¬ŅŅ³µ¾ąĄėBµŲµÄ¾ąĄėĪŖ_____£Økm£©£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com