
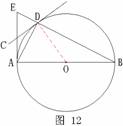
如图12,AB是⊙O的直径,经过圆上点D的直线CD恰使∠ADC=∠B.
(1) 求证:直线CD是⊙O的切线;
(2) 过点A作直线AB的垂线交BD的延长线于点E,且AB=5,BD=2,求线段AE的长.
科目:初中数学 来源: 题型:
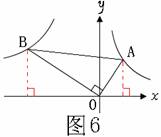
如图6,已知第一象限内的点A在反比例函数y = 2x的图象上,第二象限内的点B在反比例函数 y = kx的图象上,且OA⊥0B ,cotA= 33,则k的值为
A.-3 B.-6 C.- 3 D.-23
查看答案和解析>>
科目:初中数学 来源: 题型:
如图15.1,已知抛物线C经过原点,对称轴x=-3与抛物线相交于第三象限的点M,与x轴相交于点N,且tan∠MON = 3.
(1)求抛物线C的解析式;
(2)将抛物线C绕原点O旋转180º得到抛物线C’,抛物线C’与x轴的另一交点为A,B为抛物线C’上横向坐标为2的点. www.12999.com
①若P为线段AB上一动点,PD⊥y轴于点D,求△APD面积的最大值;
 ②过线段OA上的两点E、F分别作x轴的垂线,交折线 O –B -A于点E1、F1,再分别以线段EE1、FF1为边作如图15.2所示的等边△EE1E2、等边△FF1F2,点E以每秒1个单位长度的速度从点O向点A运动,点F以每秒1个单位长度的速度从点A向点O运动,当△EE1E2有一边与△FF1F2的某一边在同一直线上时,求时间t的值.
②过线段OA上的两点E、F分别作x轴的垂线,交折线 O –B -A于点E1、F1,再分别以线段EE1、FF1为边作如图15.2所示的等边△EE1E2、等边△FF1F2,点E以每秒1个单位长度的速度从点O向点A运动,点F以每秒1个单位长度的速度从点A向点O运动,当△EE1E2有一边与△FF1F2的某一边在同一直线上时,求时间t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
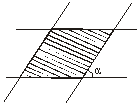
如图,两条宽度均为40m的公路相交成α角,那么这两条公路在相交处的公
共部分(图中阴影部分)的路面面积是 ( )
A、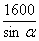 (m2) B、
(m2) B、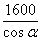 (m2) C、1600sinα(m2) D、1600cosα(m2)
(m2) C、1600sinα(m2) D、1600cosα(m2)
| |
| |
查看答案和解析>>
科目:初中数学 来源: 题型:
把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中随机抽取一张.
(1)试求取出的两张卡片数字之和为奇数的概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com