
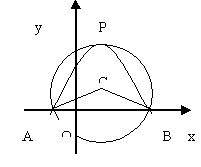
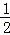 x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的坐标是(1,0),点B的坐标是(﹣3,0).
x2+mx+n交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的坐标是(1,0),点B的坐标是(﹣3,0).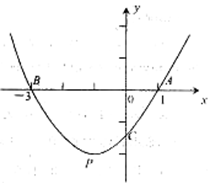
 ,
, )].
)].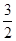 ;(2)直线PC的解析式为y=
;(2)直线PC的解析式为y=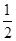 x-
x-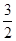 .
.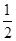 (x+3)(x-1),然后展开整理为一般式即可得到m、n的值;
(x+3)(x-1),然后展开整理为一般式即可得到m、n的值;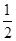 (x+3)(x-1)=
(x+3)(x-1)=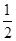 x2+x-
x2+x-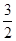 ,
,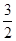 ;
;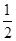 x2+x-
x2+x-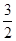 ,
,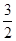 ),
),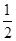 x2+x-
x2+x-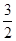 得y=
得y=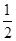 -1-
-1-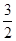 =-2,
=-2,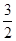 )代入得
)代入得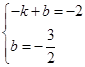 ,解得
,解得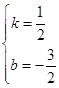
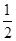 x-
x-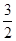 .
.

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
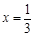 ,小亮通过观察得出了下面四条信息:
,小亮通过观察得出了下面四条信息: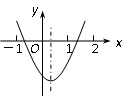
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
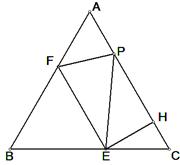
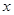 的代数式表示);
的代数式表示);查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
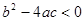 ;④-+>0; ⑤4+2+>0,错误的个数有
;④-+>0; ⑤4+2+>0,错误的个数有
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
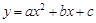 的特征数,下面给出特征数为 [2m,1-m,-1-m]的函数的一些结论:
的特征数,下面给出特征数为 [2m,1-m,-1-m]的函数的一些结论: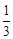 ,
,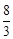 );
);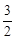 ;
;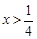 时,y随x的增大而减小;
时,y随x的增大而减小;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com