
����Ŀ����ͼ����֪��O��ֱ��AB�ϣ���һ��ֱ�����ǰ��ֱ�Ƕ�����ڵ�O����������OCD=60�㣬��OEF=45������OC��OE��ֱ��AB�ϣ�
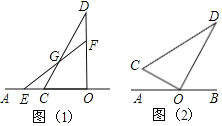
��1����ͼ��1������CD��EF�ཻ�ڵ�G������DGF�Ķ�����______�㣻
��2����ͼ��1���е����ǰ�OCD�Ƶ�O˳ʱ����ת30����ͼ��2��λ��
���������ǰ�OEF�Ƶ�O˳ʱ����ת180�����ڴ˹����У�����COE=��EOD=��DOFʱ������AOE�Ķ�����
���������ǰ�OEF�Ƶ�O��ÿ��4�����ٶ�˳ʱ����ת180�������ͬʱ�������ǰ�OCD�Ƶ�O��ÿ��1�����ٶ�˳ʱ����ת�������ǰ�OEF��ת���յ�λ��ʱ�����ǰ�OCDҲֹͣ��ת������תʱ��Ϊt�룬��OD��EFʱ����t��ֵ��
���𰸡���1��15����2��������COE=��EOD=��DOFʱ����AOE=75�㣻����OD��EFʱ��t��ֵΪ25��
��������
��1��������������ǵ����ʼ��ɵõ����ۣ�
��2������ͼ2��������֪���������COE=��EOD=45�����õ���AOE=��AOC+��COE=30��+45��=75��������COE=��EOD=��DOFʱ����ý��ۣ��ڸ��ݴ�ֱ�Ķ���õ�OD��EF���õ���OHE=90���з�����ý��ۣ�
��1���ߡ�EFO=45�㣬��D=30�㣬
���DGF=��EFO-��D=45��-30��=15�㣬
�ʴ�Ϊ��15��
��2������ͼ2��

�ߡ�COE=��EOD=��DOF����COE+��EOD=��COD����COD=90�㣬
���COE=��EOD=45�㣬
���AOE=��AOC+��COE=30��+45��=75�㣬
����COE=��EOD=��DOFʱ����AOE=75�㣻
�ڡߡ�AOE=4t�㣬��AOC=30��+t������ͼ3��
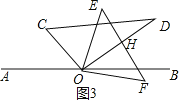
��OD��EF��
���OHE=90��
�ߡ�E=45�㣬��COD=90�㣬
���COE=45�㣬
���AOE-��AOC=��COE=45�㣬
��4t-��30+t��=45��
��t=25��
����OD��EFʱ��t��ֵΪ25��


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д� �Ƹ������������ϵ�д�
�Ƹ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ���ǽPQ��������ֱ����ľ��AB��CD �� ijһʱ����̫�����£�ľ��CD��Ӱ�Ӹպò����ڹ��ǽPQ�ϣ�
��1������ͼ�л�����ʱ��̫������CE��ľ��AB��Ӱ��BF��
��2����AB=6�ף�CD=3�� �� CD��PQ�ľ���DQ�ij�Ϊ4�ף����ʱľ��AB��Ӱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У�DΪBC�е㣬BE��CF������AE�ֱ��ཻ�ڵ�E��F������AE��������D��.
��1����ͼ�٣���BE��CFʱ������ED���ӳ���CF�ڵ�H. ��֤���ı���BECH��ƽ���ı��Σ�
��2����ͼ�ڣ���BE��AE�ڵ�E��CF��AE�ڵ�Fʱ���ֱ�ȡAB��AC���е�M��N������ME��MD��NF��ND. ��֤����EMD=��FND.


ͼ�� ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y��2x��2a��y����x��b��ͼ������A(��2��a)������x��ֱ���B��C���������ABC�����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С���ó�Ϊ3.2m��������������߲���ѧУ��˵ĸ߶ȣ��ƶ���ͣ�ʹ��͡���˶��˵�Ӱ��ǡ�����ڵ����ͬһ�㣮��ʱ���������һ�����8m����������22m������˵ĸ�Ϊ�������� 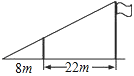
A.12m
B.10m
C.8m
D.7m
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����С���A�س������ڶ�������Ĺ�·�ϼ�����·������涨����ʻΪ����������ʻΪ����һ�����ߴ���ʻ����¼���£���λ��km��
��1�� | ��2�� | ��3�� | ��4�� | ��5�� | ��6�� | ��7�� |
��4 | +7 | ��9 | +8 | +6 | ��5 | ��2 |
���չ�ʱ��A�ض�Զ���ڵڼ��μ�¼ʱ��A����Զ��
A. 2ǧ�� ��1�� B. 1ǧ�� ��2��
C. 2ǧ�� ��4�� D. 1ǧ�� ��5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵������ȷ�ĸ���Ϊ�� ��
����aһ���Ǹ�������һ�������������������Ƿ��������κ�һ����������ƽ�������������ܵ���������������������1���ݾ���ֵ����������������0�����κ�һ���������ľ���ֵ��������
A. 0 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��һ������¥�IJ������ס��ҡ�������ѧ���������ѡ�����е�ij��¥��IJ����òͣ���ס��ҡ�������ѧ����ͬһ��¥������ò͵ĸ���Ϊ()
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߶�AB=4����O���߶�AB�ϵĵ�����C��D���߶�OA��OB���е���С�������ɵ����CD=2.
![]()
(1)С���ڷ�˼������ͻ������:����O�˶����߶�AB���ӳ���������ԭ�еĽ�����CD=2���Ƿ���Ȼ������?���С������ͼ�η�������˵������.
(2)����O�˶���ֱ��AB��ʱ��������CD=2���Ƿ���?�����ÿ̶ȳ���֤��IJ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com