
分析 选择甲设想,根据题意得出y关于x的解析式,并求出x的取值范围.(1)将y=0代入解析式中,即可求得结论;(2)两车相距70km,即y=±70,代入解析式即可求得x的值.
解答 解:选择甲同学的设想.
乙车出发时,甲车已行走的路程=60×0.5=30km.
甲车到B地还需要的时间=(310-30)÷60=4$\frac{2}{3}$小时,
乙车到A地需要时间=310÷80=3$\frac{7}{8}$小时.
故0≤x≤3$\frac{7}{8}$.
根据题意可知y=310-30-(60+80)x=-140x+280(0≤x≤3$\frac{7}{8}$).
(1)令y=0,有0=-140x+280,
解得x=2.
故乙车出发后2小时和甲车相遇.
(2)令y=70,有70=-140x+280,
解得x=1.5.
令y=-70,有-70=-140x+280,
解得x=2.5.
故当乙车出发1.5或2.5小时时,两车相距70km.
点评 本题考查了一次函数的应用,解题的关键是:选择甲同学的设想,根据题意得出y关于x的解析式.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB(指半圆和直角三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是( )
如图,在直角三角形ABC中,∠ACB=90°,CA=4.点P是半圆弧AC的中点,连接BP,线段BP把图形APCB(指半圆和直角三角形ABC组成的图形)分成两部分,则这两部分面积之差的绝对值是( )| A. | 2 | B. | 4 | C. | 1.5π-2 | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
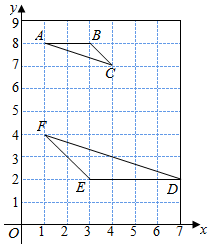 如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,是由一些大小相同的小正方体组成的几何体的主视图和俯视图.
如图所示,是由一些大小相同的小正方体组成的几何体的主视图和俯视图.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,AB=1,(AD>AB)在BC上取一点E,沿AE将△ABE向上折叠,使点B落在AD上的点F,若四边形EFDC与原矩形相似,则AD的长度为$\frac{1+\sqrt{5}}{2}$.
如图,在矩形ABCD中,AB=1,(AD>AB)在BC上取一点E,沿AE将△ABE向上折叠,使点B落在AD上的点F,若四边形EFDC与原矩形相似,则AD的长度为$\frac{1+\sqrt{5}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com