
【题目】如图1,有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN于点Q,连接CM.
(1)求证:四边形CMPN是菱形;
(2)当P,A重合时,如图2,求MN的长;
(3)设△PQM的面积为S,求S的取值范围.

【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)首先利用矩形的性质得出PM∥CN,然后根据平行线的性质和折叠的性质得出PM=CN,利用一组对边平行且相等的四边形是平行四边形证明四边形CMPN是平行四边形,再根据NC=NP即可证明结论;
(2)设BN=x,则AN=NC=8-x,首先利用勾股定理求出x的值,进而求出NC的长度,然后利用勾股定理求出AC的长度,最后利用菱形的面积公式求解即可;
(3)根据菱形的对称性可知S=![]() ,只要找到菱形CMPN的面积的最大值和最小值即可,又因为S菱形CMPN=CN·AB,所以只需找到CN的最大值和最小值即可,当点M与点D重合时,此时CN最短,当点P与点A重合时,CN最长,代入计算即可得出答案.
,只要找到菱形CMPN的面积的最大值和最小值即可,又因为S菱形CMPN=CN·AB,所以只需找到CN的最大值和最小值即可,当点M与点D重合时,此时CN最短,当点P与点A重合时,CN最长,代入计算即可得出答案.
(1)证明:∵四边形ABCD是矩形,
∴PM∥CN,
∴∠PMN=∠MNC.
由折叠的性质可知∠MNC=∠PNM,NC=NP,
∴∠PMN=∠PNM.
∴PM=PN.
∵NC=NP,
∴PM=CN.
∵MP∥CN,
∴四边形CMPN是平行四边形.
∵NC=NP,
∴四边形CMPN是菱形.
(2)当点P与点A重合时,设BN=x,则AN=NC=8-x.
在Rt△ABN中,AB2+BN2=AN2,
即42+x2=(8-x)2,解得x=3.
∴CN=8-3=5.
∵四边形CMPN是菱形,AC=![]() ,
,
∴MN=![]() .
.
(3)∵四边形CMPN是菱形,
∴S=![]()
∵S菱形CMPN=CN·AB,

∴当点M与点D重合时,如图,此时CN最短,菱形CMPN的面积最小,
∵![]() ,四边形CMPN是菱形,
,四边形CMPN是菱形,
∴四边形CMPN是正方形,
则S最小=![]() ;
;
当点P与点A重合时,CN最长,菱形CMPN的面积最大,
则S最大=![]() ×5×4=5.
×5×4=5.
∴S的取值范围是![]() .
.


科目:初中数学 来源: 题型:
【题目】(1)已知一个多边形的内角和是它的外角和的 3 倍,求这个多边形的边数.
(2)如图,点F 是△ABC 的边 BC 延长线上一点.DF⊥AB,∠A=30°,∠F=40°,求∠ACF 的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求,解答下列问题.
(1)解下列方程组(直接写出方程组的解即可):
A.![]() B.
B.![]() C.
C.![]()
方程组A的解为 ,方程组B的解为 ,方程组C的解为 ;
(2)以上每个方程组的解中,x值与y值的大小关系为 ;
(3)请你构造一个具有以上外形特征的方程组,并直接写出它的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把下面证明过程补充完整:
已知:如图,∠ADC=∠ABC,BE、DF分别平行∠ABC、∠ADC,且∠1=∠2.
求证:∠A=∠C.
证明:因为BE、DF分别平分∠ABC、∠ADC,( ).
所以∠1=![]() ∠ABC,∠3=
∠ABC,∠3=![]() ∠ADC( ).
∠ADC( ).
因为∠ABC=∠ADC(已知),
所以∠1=∠3( ),
因为∠1=∠2(已知),
所以∠2=∠3( ).
所以 ∥ ( ).
所以∠A+∠ =180°,∠C+∠ =180°( ).
所以∠A=∠C( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 和
和![]() 都是边长为1的等边三角形.
都是边长为1的等边三角形.
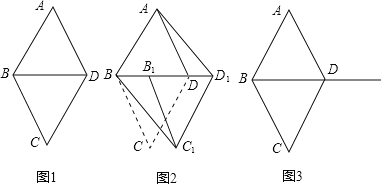
![]() 四边形ABCD是菱形吗?为什么?
四边形ABCD是菱形吗?为什么?
![]() 如图2,将
如图2,将![]() 沿射线BD方向平移到
沿射线BD方向平移到![]() 的位置,则四边形
的位置,则四边形![]() 是平行四边形吗?为什么?
是平行四边形吗?为什么?
![]() 在
在![]() 移动过程中,四边形
移动过程中,四边形![]() 有可能是矩形吗?如果是,请求出点B移动的距离
有可能是矩形吗?如果是,请求出点B移动的距离![]() 写出过程
写出过程![]() ;如果不是,请说明理由
;如果不是,请说明理由![]() 图3供操作时使用
图3供操作时使用![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】共有1500kg化工原料,由A,B两种机器人同时搬运,其中,A型机器人比B型机器每小时多搬运30kg,A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等,问需要多长时间才能运完?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了庆祝校园艺术节,准备购买一批盆花布置校园.已知1盆A种花和2盆B种花一共需13元,2盆A种花和1盆B种花一共需11元.
(1)求1盆A种花和1盒B种花的售价各是多少元?
(2)学校准备购进这两种盆花共100盆,并且A种盆花的数量不超过B种盆花数量的2倍,请求出A种盆花的数量最多是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com