练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    已知：如图，△ABC中，∠ACB=90°，CD⊥AB于D，AB=10，BC=6．求：sin∠ACD的值及AD的长．
    考点：解直角三角形
    专题：
    分析：根据勾股定理可以求得AC的长度，即可求得sin∠ACD的值，再根据AC的长即可求得AD的长．
    解答：解：∵CD⊥AB，∠ACB=90°，
    ∴∠B=∠ACD，
    RT△ABC中，AC=
    		AB2-BC2
    =8，
    ∴sin∠ACD=sinB=
    AC
    AB
    =
    4
    5
    ，
    ∴AD=AC•sin∠ACD=
    32
    5
    ．
    点评：本题考查了直角三角形中正弦值的计算，考查了勾股定理的运用，本题中求AC的长是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知CA、BE分别垂直AB于A点和B点，∠CDE=90°，
    （1）求证：△CAD∽△DBE；
    （2）若CA=2，AD=3，BE=6，求DB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，Rt△ABC中，∠BAC=90°，∠ACB=30°，点A的坐标为（3，0），过点B的双曲线y=
    k
    x
    （x＞0）恰好经过BC中点D．则k值为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

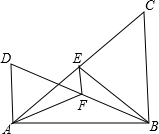    如图，∠ABC=∠BAD=90°，点E，F分别是AC，BC的中点．
    （1）求证：∠EAF=∠EBF；
    （2）试判断直线EF与AB的位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，矩形ABCD的面积为1，它的两条对角线交于点O1，取BO1的中点O2，连AO2并延长到C1，使得AO2=C1O2，得到四边形ABC1O1，同样取BO2的中点O3，连AO3并延长到C2，使得AO3=C2O3，得到四边形ABC2O2…依此类推，可作得四边形ABCnOn．
    （1）四边形ABC1DO1的类型是
     
    ；
    （2）四边形ABCnOn的面积为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，已知：⊙O中AB是直径，点P在AB上，PB平分∠CPD，求证：PC=PD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一种树苗的高度用h表示，树苗生长的年数用a表示，测得的有关数据如下表（树苗原高度为100厘米）：
    （1）写出用年数a表示高度h的关系式；
    （2）利用（1）题的关系式计算生长了6年的树苗的高度．
    年数a/年高度h/cm
    1100+5
    2100+10
    3100+15
    4100+20
    ……

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC中，∠C=90°，∠A=30°，已知AC=3，求周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

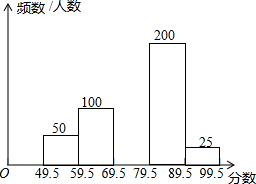    某市为了解参加历史科结业的2万名学生的考试成绩情况，现从中随机抽取部分学生的成绩作为一个样本，整理后分成5组，绘制了频数分布直方图，其中，第二组的频率为0.2．
    （1）求成绩在70-80分的学生人数，并补全频数分布直方图．
    （2）抽取的样本中，学生结业成绩的，中位数落在第几小组？并说明理由．
    （3）若成绩在80分以上为优秀，请你估计全市参加考试的学生中成绩优秀的人数．

    查看答案和解析>>

    同步练习册答案