
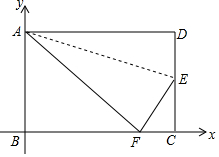
 ��ͼ������ABCD��AE�۵���ʹD���ڱ�BC�ϵ�F�㴦����AB=8��BC=10�Ե�BΪ����ԭ��BCΪx�ᣬABΪy�ᣬ����ֱ������ϵ��
��ͼ������ABCD��AE�۵���ʹD���ڱ�BC�ϵ�F�㴦����AB=8��BC=10�Ե�BΪ����ԭ��BCΪx�ᣬABΪy�ᣬ����ֱ������ϵ������ ��1���ɡ�AEF���ɡ�ADE���۵õ�������AD=AF=10��EF=ED����DE=EF=x����Rt��ABF�У�BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6����Rt��EFC�У���EF2=EC2+CF2�г����̼��ɽ�����⣮
��2�����ֱ��AE��DF�Ľ���ʽ���ⷽ���鼴�ɣ�
��3��ֻҪ֤����AFP�ǵ��������μ��ɽ�����⣮
��4�����ô���ϵ�������ɽ����
��5�����������ο��Ǽ��ɢټ�ͼ1���ڼ�ͼ2��
��� �⣺��1����ͼ1�У����ı���ABCD�Ǿ��Σ�
��AB=CD=8��BC=0D=10����D=��BCD=��ABC=90�㣬
�ߡ�AEF���ɡ�ADE���۵õ���
��AD=AF=10��EF=ED����DE=EF=x��
��Rt��ABF��BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6��
��CF=BC-BF=4��
��Rt��EFC����EF2=EC2+CF2��
��x2=��8-x��2+42��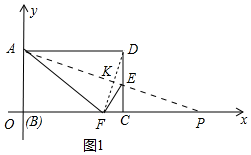
��x=5��
��DE=EF=5��EC=3��
���E���꣨10��3����
�ʴ�Ϊ��10��3����
��2����ͼ1�У���A��0��8����E��10��3����
��ֱ��AE�Ľ���ʽΪy=-$\frac{1}{2}$x+8��
��F��6��0����D��10��8����
��ֱ��DF�Ľ���ʽΪy=2x-12��
��$\left\{\begin{array}{l}{y=-\frac{1}{2}x+8}\\{y=2x-12}\end{array}\right.$���$\left\{\begin{array}{l}{x=8}\\{y=4}\end{array}\right.$��
���ۺ���DF���������Ϊ��8��4����
�ʴ�Ϊ��8��4����
��3����ͼ1�У���AD��PC��
���DAP=��APF=��FAP��
��FA=FP=10��
��OP=OF+FP=16����AFP�ǵ��������Σ�
��P������16��0����
�ʴ𰸷ֱ�Ϊ���������Σ���16��0����
��4����ֱ��AE�Ľ���ʽΪy=kx+b����A��0��8����E��10��3������õ�$\left\{\begin{array}{l}{b=8}\\{10k+b=3}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=8}\end{array}\right.$��
��ֱ��AE�Ľ���ʽΪy=-$\frac{1}{2}$x+8��
�ʴ�Ϊy=-$\frac{1}{2}$x+8��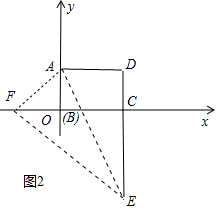
��5����ͼ2�У�����E��DC���ӳ�����ʱ��
�ߡ�AEF���ɡ�ADE���۵õ���
��AF=AD=10��EF=DE����EF=ED=x��
��Rt��AFO��OF=$\sqrt{A{F}^{2}-O{A}^{2}}$=6��
��CF=16��F��-6��0����
��Rt��ECF����EF2=CF2+CE2��
��x2=162+��x-8��2��
��x=20��
��CE=12��E��10��-12����
��ֱ��AE�Ľ���ʽΪy=kx+b����$\left\{\begin{array}{l}{b=8}\\{10k+b=-12}\end{array}\right.$��
���$\left\{\begin{array}{l}{k=-2}\\{b=8}\end{array}\right.$��
��ֱ��AE�Ľ���ʽΪy=-2x+8��
������������F������Ϊ��-6��0����6��0����ֱ��AE�Ľ���ʽΪy=-2x+8��y=-$\frac{1}{2}$x+8��
�ʴ�Ϊ��-6��0����6��0����y=-2x+8��y=-$\frac{1}{2}$x+8��
���� ���⿼���ı����ۺ��⡢һ�κ��������ɶ��������۱任��֪ʶ������Ĺؼ��ǣ����������ѧ֪ʶ������⣬ѧ���÷��̵�˼��˼�����⣬�����п��������ͣ�


 ������ȫ��������ϵ�д�
������ȫ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
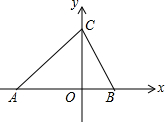 ��ͼ����ƽ��ֱ������ϵ�У�A��-4��0����B��2��0������C��y���������ϣ���S��ABC=18��
��ͼ����ƽ��ֱ������ϵ�У�A��-4��0����B��2��0������C��y���������ϣ���S��ABC=18���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | $\sqrt{7}$ | C�� | 5��$\sqrt{7}$ | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
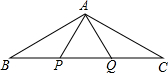 ��֪����P��Q�ǡ�ABC�ı�BC�ϵ������㣬��BP=PQ=QC=AP=AQ����BAC�Ķ����ǣ�������
��֪����P��Q�ǡ�ABC�ı�BC�ϵ������㣬��BP=PQ=QC=AP=AQ����BAC�Ķ����ǣ�������| A�� | 100�� | B�� | 120�� | C�� | 130�� | D�� | 150�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
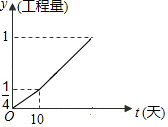 �ס��������̶����ij��̣���������10�죬Ȼ���Ҽ�����������ʣ�µĹ��̣��蹤������Ϊ1�������ܹ�����y������t֮��Ĺ�ϵΪy=kx-$\frac{1}{6}$�������̽�����ͼ��ʾ����ʵ�������������õ�ʱ��ȼ�����ɴ�������õ�ʱ����12�죮
�ס��������̶����ij��̣���������10�죬Ȼ���Ҽ�����������ʣ�µĹ��̣��蹤������Ϊ1�������ܹ�����y������t֮��Ĺ�ϵΪy=kx-$\frac{1}{6}$�������̽�����ͼ��ʾ����ʵ�������������õ�ʱ��ȼ�����ɴ�������õ�ʱ����12�죮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com