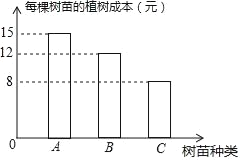
【题目】现种植A、B、C三种树苗一共480棵，安排80名工人一天正好完成，已知每名工人只植一种树苗，且每名工人每天可植A种树苗8棵；或植B种树苗6棵，或植C种树苗5棵．经过统计，在整个过程中，每棵树苗的种植成本如图所示．设种植A种树苗的工人为x名，种植B种树苗的工人为y名．
（1）求y与x之间的函数关系式；
（2）设种植的总成本为w元，
①求w与x之间的函数关系式；
②若种植的总成本为5600元，从植树工人中随机采访一名工人，求采访到种植C种树苗工人的概率．
【答案】（1）
；（2）①
；②
【解析】
（1）先求出种植C种树苗的人数，根据现种植A、B、C三种树苗一共480棵，可以列出等量关系，解出y与x之间的关系；
（2）①分别求出种植A，B，C三种树苗的成本，然后相加即可；
②求出种植C种树苗工人的人数，然后用种植C种树苗工人的人数÷总人数即可求出概率．
解：（1）设种植A种树苗的工人为x名，种植B种树苗的工人为y名，则种植C种树苗的人数为（80-x-y）人，
根据题意，得：8x+6y+5（80-x-y）=480，
整理，得：y=-3x+80；
（2）①w=15×8x+12×6y+8×5（80-x-y）=80x+32y+3200，
把y=-3x+80代入，得：w=-16x+5760，
②种植的总成本为5600元时，w=-16x+5760=5600，
解得x=10，y=-3×10+80=50，
即种植A种树苗的工人为10名，种植B种树苗的工人为50名，种植B种树苗的工人为：80-10-50=20名．
采访到种植C种树苗工人的概率为：
=．
每日10分钟口算心算速算天天练系列答案科目：初中数学 来源： 题型：
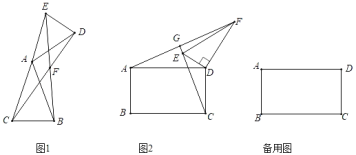
【题目】（1）如图1，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝30°，连接CD，BE交于点F．
＝ ；∠BFD＝ ；
（2）如图2，在矩形ABCD和△DEF中，AB＝
AD，∠EDF＝90°，∠DEF＝60°，连接AF交CE的延长线于点G．求
的值及∠AGC的度数，并说明理由．
（3）在（2）的条件下，将△DEF绕点D在平面内旋转，AF，CE所在直线交于点P，若DE＝1，AD＝
，求出当点P与点E重合时AF的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将矩形ABCD绕点B顺时针旋转得到矩形A1BC1D1，点A、C、D的对应点分别为A1、C1、D1．
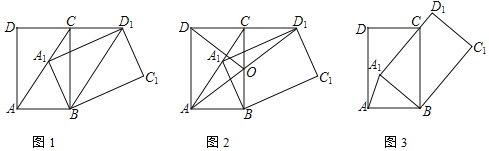
（1）当点A1落在AC上时：
①如图1，若∠CAB＝60°，求证：四边形ABD1C为平行四边形；
②如图2，AD1交CB于点O，若∠CAB≠60°，求证：DO＝AO；
（2）如图3，当A1D1过点C时，若BC＝10，CD＝6，直接写出A1A的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
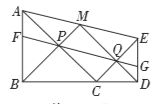
【题目】如图，在线段
上任取一点
，将线段
逆时针旋转
得到线段
，将线段
顺时针旋转得到线段
，连接
，
，
，
是的中点，连接
交于点
，连接
交于点
．直线
分别交，于
，
两点，有下列结论：①
；②四边形
为平行四边形；③
；④
．其中正确的结论是（ ）
A.①③④B.①②③C.②③④D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
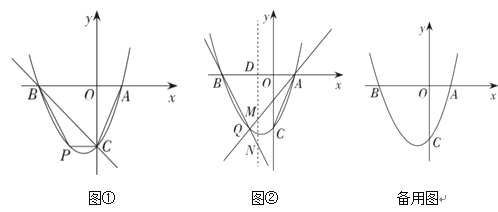
【题目】如图①，直线
分别与
轴、
轴交于点
，
，抛物线
经过，两点，且与轴的另一交点为
．
（1）求抛物线的函数解析式；
（2）如图①，点
在第三象限内的抛物线上．
①连接
，
，
，当四边形
的面积最大时，求点的坐标；
②
为轴上一点，当
取得最小值时，求点的坐标；
（3）如图②，
为轴下方抛物线上任意一点，
是抛物线的对称轴与轴的交点，直线
，
分别交抛物线的对称轴于点
，
．问：
是否为定值？如果是，请求出这个定值；如果不是，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某数学兴趣小组研究我国古代《算法统宗》里这样一首诗：我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．诗中后两句的意思是：如果每一间客房住7人，那么有7人无房可住；如果每一间客房住9人，那么就空出一间房．
（1）求该店有客房多少间？房客多少人？
（2）假设店主李三公将客房进行改造后，房间数大大增加．每间客房收费20钱，且每间客房最多入住4人，一次性定客房18间以上（含18间），房费按8折优惠．若诗中“众客”再次一起入住，他们如何订房更合算？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为确保信息安全，信息需加密传输，发送方由明文→密文(加密)，接收方由密文→明文(解密)，已知有一种键盘密码，每个字母与所在按键的数字序号对应(见如图)，如字母
与数字序号0对应，当明文中的字母对应的序号为
时，将
除以26后所得的余数作为密文中的字母对应的序号，例如明文“
”对应密文“
”
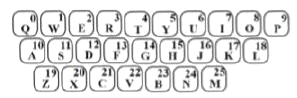
按上述规定，将密文“
” 解密成明文后是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】现有以下命题：
①如果三角形的三个内角的度数比是
，那么这个三角形是直角三角形；
②如果不等式
的解集为
，那么
；
③若将一次函数
的图象向上平移3个单位，则平移所得直线不经过第四象限；
④命题“对角线互相垂的四边形是菱形”的逆命题．
则真命题的个数为（ ）．
A.0个B.1个C.2个D.3个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某地向湖北派遣由5名医护人员组成的一支医疗队，支援抗击新型冠状病毒肺炎疫情．已知这五名医护人员的年龄分别为24，28，36，36，47（单位：岁），其中年龄为24，47岁的是女队员，其余是男队员．
（1）求这五名医护人员的年龄的众数；
（2）若因疫情需要，需增加一名医护人员，若增加后年龄的中位数小于原来年龄的中位数，则增加医护人员的最大年龄是多少？
（3）若需要从男性队员中选两名参加重症病人抢救，求所选两名队员的年龄恰好相等的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com