
【题目】如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,﹣1),反比例函数y= ![]() (x>0)的图象经过线段MN的中点A.
(x>0)的图象经过线段MN的中点A. 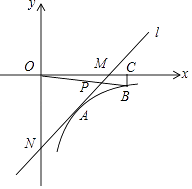
(1)求直线l和反比例函数的解析式;
(2)在函数y= ![]() (x>0)的图象上取不同于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P,若△ONP的面积是△OBC的面积的3倍,求点P的坐标.
(x>0)的图象上取不同于点A的一点B,作BC⊥x轴于点C,连接OB交直线l于点P,若△ONP的面积是△OBC的面积的3倍,求点P的坐标.
【答案】
(1)解:设直线l的解析式为y=mx+n(m≠0),
将(3,0)、(0,﹣1)代入y=mx+n,
![]() ,解得:
,解得: 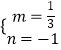 ,
,
∴直线l的解析式为y= ![]() x﹣1.
x﹣1.
∵点A为线段MN的中点,
∴点A的坐标为( ![]() ,﹣
,﹣ ![]() ).
).
将A( ![]() ,﹣
,﹣ ![]() )代入y=
)代入y= ![]() ,
,
![]() =﹣
=﹣ ![]() ,解得:k=﹣
,解得:k=﹣ ![]() ,
,
∴反比例函数解析式为y=﹣ ![]()
(2)解:∵S△OBC= ![]() |k|=
|k|= ![]() ,
,
∴S△ONP=3S△OBC= ![]() .
.
∵点N(0,﹣1),
∴ON=1.
设点P的坐标为(a, ![]() a﹣1)(0<a<3),
a﹣1)(0<a<3),
∴S△ONP= ![]() ONa=
ONa= ![]() a=
a= ![]() ,
,
∴a= ![]() ,
, ![]() a﹣1=﹣
a﹣1=﹣ ![]() ,
,
∴点P的坐标为( ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)根据点M、N的坐标利用待定系数法即可求出直线l的解析式,根据点A为线段MN的中点即可得出点A的坐标,根据点A的坐标利用待定系数法即可求出反比例函数解析式;(2)根据反比例函数系数k的几何意义即可求出S△OBC的面积,设点P的坐标为(a, ![]() a﹣1)(0<a<3),根据三角形的面积公式结合S△ONP的面积即可求出a值,进而即可得出点P的坐标.
a﹣1)(0<a<3),根据三角形的面积公式结合S△ONP的面积即可求出a值,进而即可得出点P的坐标.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】如图是某超市地下停车场入口的设计图,请根据图中数据计算CE的长度.(结果保留小数点后两位;参考数据:sin22°=0.3746,cos22°=0.9272,tan22°=0.4040) 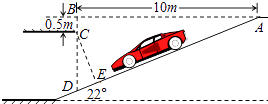
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中. 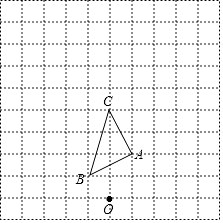
(1)以图中的点O为位似中心,在网格中画出△ABC的位似图形△A1B1C1 , 使△A1B1C1与△ABC的位似比为2:1;
(2)若△A1B1C1的面积为S,则△ABC的面积是
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.
(1)求出y与x的函数关系式,并写出自变量x的取值范围.
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式.
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是AC边上一点,且AD=2DC,E是AB边上一点,ED与BC的延长线相交于点F,且BC=CF,G是EF的中点,连接CG,若CG=2,求AB的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是二次函数y=ax2+bx+c图象的一部分,其对称轴为直线x=1,若其与x轴交于点为A(3,0),则由图象可知,方程ax2+bx+c的另一个解是( ) 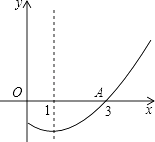
A.﹣1
B.﹣2
C.﹣1.5
D.﹣2.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角△ABC中,边BC长为12,高AD长为8.
(1)如图,矩形EFGH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K. 
①求 ![]() 的值;
的值;
②设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值;
(2)若AB=AC,正方形PQMN的两个顶点在△ABC一边上,另两个顶点分别在△ABC的另两边上,直接写出正方形PQMN的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com