
分析 (1)、(2)根据二次根式的混合运算法则进行计算即可;
(3)、(4)根据分式的混合运算法则进行计算即可.
解答 解:(1)$\frac{2}{3}$$\sqrt{32}$÷(-$\frac{2}{3}$$\sqrt{6}$)×$\frac{1}{6}$$\sqrt{24}$=-$\frac{8\sqrt{2}}{3}$×$\frac{3}{2\sqrt{6}}$×$\frac{2\sqrt{6}}{6}$=-$\frac{4\sqrt{2}}{3}$;
(2)$\sqrt{2}$×$\sqrt{32}$+${(\sqrt{2}-1)}^{2}$=8+2-2$\sqrt{2}$+1=11-2$\sqrt{2}$;
(3)a-1-$\frac{{a}^{2}}{a+1}$=$\frac{(a-1)(a+1)-{a}^{2}}{a+1}$=-$\frac{1}{a+1}$;
(4)(a-$\frac{2a-1}{a}$)÷$\frac{1{-a}^{2}}{{a}^{2}+a}$•$\frac{a-1}{{a}^{2}-2a+1}$=$\frac{{a}^{2}-2a+1}{a}$×$\frac{a(a+1)}{(1-a)(1+a)}$×$\frac{a-1}{{a}^{2}-2a+1}$=-1.
点评 此题考查了二次根式的混合运算,分式的混合运算,熟练掌握运算法则是解本题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
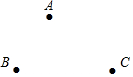 如图,已知点A、B、C.
如图,已知点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
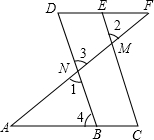 在横线上填出正确的结论,括号内写上理由已知:∠1=∠2,∠A=∠F.求证:∠C=∠D.
在横线上填出正确的结论,括号内写上理由已知:∠1=∠2,∠A=∠F.求证:∠C=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
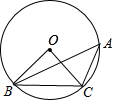 如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则BC的长为( )
如图,点A、B、C在⊙O上,若∠BAC=45°,OB=2,则BC的长为( )| A. | 2 | B. | 4 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com