
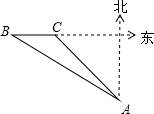
 如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )
如图,海关缉私艇在A处接到情报,在A的北偏西60°方向的B处发现一艘可疑船只正以24海里/时的速度向正东方向航行,于是该艇立即沿北偏西45°的方向前进,经过1小时航行,恰好在C处截住可疑船只,则缉私艇的速度为( )| A. | (12$\sqrt{2}$+12$\sqrt{6}$)海里/时 | B. | (12$\sqrt{3}$+12$\sqrt{6}$)海里/时 | C. | (12$\sqrt{2}$+12$\sqrt{3}$)海里/时 | D. | (8$\sqrt{3}$+8$\sqrt{6}$)海里/时 |
分析 设AD=x海里,根据正切的概念用x表示出BD、CD,根据题意列出方程,解方程求出x,求出AC的长,得到答案.
解答 解: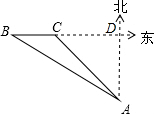 由题意得,BC=24海里,
由题意得,BC=24海里,
设AD=x海里,
在Rt△ABD中,BD=$\frac{AD}{tan∠B}$=$\sqrt{3}$x,
在Rt△ACD中,∠ACD=45°,
∴CD=AD=x,
则$\sqrt{3}$x-x=24,
解得,x=12$\sqrt{3}$+12,
∴AC=$\sqrt{2}$x=12$\sqrt{2}$+12$\sqrt{6}$,
∴缉私艇的速度为(12$\sqrt{2}$+12$\sqrt{6}$)海里/时,
故选:A.
点评 本题考查的是解直角三角形的应用,掌握锐角三角函数的概念、正确标注方向角是解题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:填空题
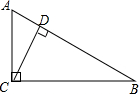 如图,∠ACB=90°,CD⊥AB,垂足为D,AB=13cm,AC=5cm,BC=12cm,那么点B到AC的距离是12cm,点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.
如图,∠ACB=90°,CD⊥AB,垂足为D,AB=13cm,AC=5cm,BC=12cm,那么点B到AC的距离是12cm,点A到BC的距离是5cm,点C到AB的距离是$\frac{60}{13}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
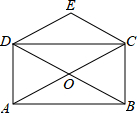 如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )
如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC,若AC=4,则四边形CODE的周长为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$-1 | D. | 2-$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | 4+±$\sqrt{2}$ | D. | 0或8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
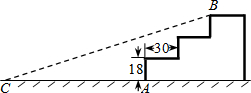 如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
如图,某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡,设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )| A. | 270cm | B. | 210cm | C. | 180cm | D. | 96cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )
如图,直角边长为$\sqrt{2}$的等腰直角三角形与边长为3的等边三角形在同一水平线上,等腰直角三角形沿水平线从左向右匀速穿过等边三角形时,设穿过时间为t,两图形重合部分的面积为S,则S关于t的图象大致为( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com