
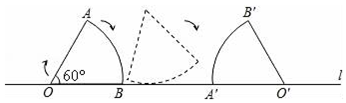
分析 仔细观察顶点O经过的路线可得,顶点O经过的路线可以分为三段,分别求出三段的长,再求出其和即可.
解答 解:顶点O经过的路线可以分为三段,当弧AB切直线l于点B时,有OB⊥直线l,此时O点绕不动点B转过了90°;
第二段:OB⊥直线l到OA⊥直线l,O点绕动点转动,而这一过程中弧AB始终是切于直线l的,所以O与转动点P的连线始终⊥直线l,所以O点在水平运动,此时O点经过的路线长=BA’=AB的弧长
第三段:OA⊥直线l到O点落在直线l上,O点绕不动点A转过了90°
所以,O点经过的路线总长S=π+$\frac{2}{3}$π+π=$\frac{8}{3}$π.
故答案为$\frac{8}{3}$π.
点评 本题考查弧长公式,关键是理解顶点O经过的路线可得,则顶点O经过的路线总长为三个扇形的弧长,记住弧长公式L=$\frac{n•π•R}{180}$是解题的关键.


科目:初中数学 来源: 题型:填空题
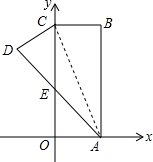 如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,4),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为(-$\frac{15}{17}$,$\frac{60}{17}$).
如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,4),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为(-$\frac{15}{17}$,$\frac{60}{17}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
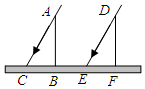 如图,已知太阳光线AC和DE是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )
如图,已知太阳光线AC和DE是平行的,在同一时刻两根高度相同的木杆竖直插在地面上,在太阳光照射下,其影子一样长.这里判断影长相等利用了全等图形的性质,其中判断△ABC≌△DFE的依据是( )| A. | SAS | B. | AAS | C. | HL | D. | ASA |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
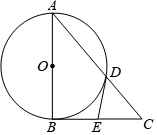 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,过点D的切线交BC于E.
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,过点D的切线交BC于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com