Question

已知：y与x成反比例，并且当x=-2时，y=-5．
（1）求y与x之间的函数关系式；
（2）直线y=mx与（1）中所求函数图象交点的横坐标是l，试求m的值；
（3）在（2）中，是否还有另外的交点？若有，请直接写出交点的坐标．

Answer 1

解：（1）设，
把x=-2，y=-5代入，得
∴k=10
∴y与x的函数关系式是．
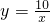
（2）把x=1代入，
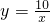
得y=10
即交点坐标为（1，10）
∴10=m×1
∴m=10
（3）另一个交点坐标为（-1，-10）．
分析：（1）设出反比例函数解析式，把x=-2时，y=-5代入即可求得函数关系式；
（2）把x=1代入反比例函数解析式可得纵坐标的值，代入直线解析式可得m的值；
（3）易得另一交点与（2）中得到的点关于原点对称．
点评：考查一次函数与反比例函数交点问题；用到的知识点为：在函数解析式上的点，适合该函数解析式；反比例函数与正比例函数的2个交点关于原点对称．