
 如图,圆柱形油槽内原有积油的水平面宽CD=60cm,油深为10cm.若油面上升10cm,则此时油面宽AB为多少?(教材124页第10题改编)
如图,圆柱形油槽内原有积油的水平面宽CD=60cm,油深为10cm.若油面上升10cm,则此时油面宽AB为多少?(教材124页第10题改编) 分析 作OE⊥CD于点E,交AB于点F,设半径是r,则OE=r-10.在直角△OCE中,根据OC2=OE2+CE2,即可列方程求得r,然后在直角△AOF中利用勾股定理求得AF的长,则AB的长即可求得.
解答 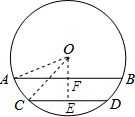 解:作OE⊥CD于点E,交AB于点F.则CE=DE=$\frac{1}{2}$×60=30(cm),
解:作OE⊥CD于点E,交AB于点F.则CE=DE=$\frac{1}{2}$×60=30(cm),
设半径是r,则OE=r-10.
在直角△OCE中,OC2=OE2+CE2,即r2=302+(r-10)2,
解得:r=50.
则OF=50-10-10=30(cm),
在直角△AOF中,AF=$\sqrt{O{A}^{2}-O{F}^{2}}$=$\sqrt{5{0}^{2}-3{0}^{2}}$=40(cm),
又∵OE⊥AB,
∴AB=2AF=80(cm).
点评 本题考查了垂径定理,在直角△OCE中利用勾股定理求得圆的半径长是解决本题的关键.


科目:初中数学 来源: 题型:解答题
 如图,把两条钢条的中点连在一起,可以做成一个测量工件槽宽的工具(卡钳).那么要测量工件内槽宽A′B′,则只要测量AB即可.
如图,把两条钢条的中点连在一起,可以做成一个测量工件槽宽的工具(卡钳).那么要测量工件内槽宽A′B′,则只要测量AB即可.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3 | B. | -$\frac{3}{2}$ | C. | 3 | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为了防洪,某地区计划将长为1000m的一堤面加宽1.5m,背水坡坡度由原来1:1改为1:2,已知原背水坡坡长AD=8.0m,求完成这一工程所需的土方.(精确到1m3,$\sqrt{2}$≈1.414)
如图,为了防洪,某地区计划将长为1000m的一堤面加宽1.5m,背水坡坡度由原来1:1改为1:2,已知原背水坡坡长AD=8.0m,求完成这一工程所需的土方.(精确到1m3,$\sqrt{2}$≈1.414)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com