
【题目】规定一种新运算:![]() ,例如:
,例如:![]() 根据理解计算下列式子的值:(0*1)+(1*2)+(2*3)+(3*4)+…+(2019*2020)
根据理解计算下列式子的值:(0*1)+(1*2)+(2*3)+(3*4)+…+(2019*2020)
科目:初中数学 来源: 题型:
【题目】《代数学》中记载,形如x2+10x=39的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为![]() x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )
x的矩形,得到大正方形的面积为39+25=64,则该方程的正数解为8-5=3”,小聪按此方法解关于x的方程x2+6x+m=0时,构造出如图2所示的图形,己知阴影部分的面积为36,则该方程的正数解为( )

A.6B.3![]() -3C.3
-3C.3![]() -2D.3
-2D.3![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2,已知点A,B是数轴上的点,请参照图并思考,完成下列各题.
(1)如果点A表示数-3,将点A向右移动7个单位长度,那么终点B表示的数是_____,A,B两点间的距离是_____;
(2)如果点A表示数3,将A点向左移动7个单位长度,再向右移动5个单位长度,那么终点表示的数是_____,A,B两点间的距离为_____;
(3)如果点A表示数-4,将A点向右移动168个单位长度,再向左移动256个单位长度,那么终点B表示的数是_____,A、B两点间的距离是_____;
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示什么数?A,B两点间的距离为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足﹣M≤y≤M,则称这个函数是有界函数,在所有满足条件的M中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.
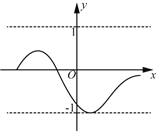
(1)分别判断函数 y=![]() (x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(x>0)和y=x+1(﹣4≤x≤2)是不是有界函数?若是有界函数,求其边界值;
(2)若函数y=﹣x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;
(3)将函数 y=x2(﹣1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时,满足![]() ≤t≤1?
≤t≤1?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,在平行四边形 ABCD 中,对角线 AC 、 BD 交于点 O ,并且 DAC 60 ,ADB 15 ,点 E 是 AD 上一动点,延长 EO 交 BC 于点 F 。当点 E 从 D 点向 A 点移动 过程中(点 E 与点 D 、点 A 不重合),则四边形 AFCE 的变化是( )
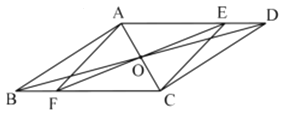
A.平行四边形→矩形→平行四边形→菱形→平行四边形
B.平行四边形→矩形→平行四边形→正方形→平行四边形
C.平行四边形→菱形→平行四边形→矩形→平行四边形
D.平行四边形→矩形→菱形→正方形→平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 分别交x轴、y轴于A、B两点,抛物线
分别交x轴、y轴于A、B两点,抛物线![]() 经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
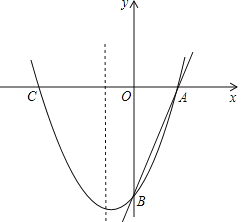
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下表,回答问题:
x | … | -2 | -1 | 0 | 1 | 2 | … |
-2x+5 | … | 9 | 7 | 5 | 3 | a | … |
2x+8 | … | 4 | 6 | 8 | 10 | b | … |
(初步感知)
(1)a= ;b= ;
(归纳规律)
(2)随着x值的变化,两个代数式的值变化规律是什么?
(问题解决)
(3)比较-2x+5与2x+8的大小;
(4)请写出一个含x的代数式,要求x的值每增加1,代数式的值减小5,当x=0时,
代数式的值为-7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1)在RtΔABC中,∠ACB=900,∠B=600,在图中作出∠ACB的三等分线CD,CE.(要求:尺规作图,保留痕迹,不定作法)
(2)由(1)知,我们可以用尺规作出直角的三等分线,但是仅仅使用尺规却不能把任意一个角分成三等分,为此,人们发明了许多等分角的机械器具,如图(2)是用三张硬纸片自制的一个最简单的三分角器,与半圆O相接的AB带的长度与半圆的半径相等:BD带的长度任意,它的一边与直线AC形成一个直角,且志半圆相切于点B,假设需要将∠KSM三等分,如图(3),首先将角的顶点S置于BD上,角的一边SK经过点A,另一边SM与半圆相切,连接SO,则SB,SO为∠KSM的三等分线,请你证明。

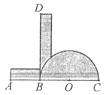

图(1) 图(2) 图(3)
查看答案和解析>>
科目:初中数学 来源: 题型:
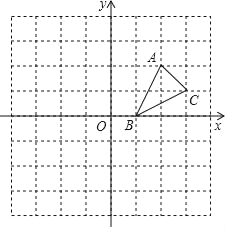
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0).
(1)画出△ABC关于x轴对称的△A1B1C1;
(2)画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2,并写出点C2的坐标;
(3)△A1B1C1与△A2B2C2成中心对称吗?若成中心对称,写出对称中心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com