
如图,抛物线 的图象与
的图象与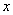 轴交于
轴交于 、
、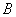 两点,与
两点,与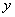 轴交于
轴交于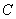 点,已知
点,已知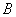 点坐标为(4,0).
点坐标为(4,0).
(1)求抛物线的解析式;
(2)试探究 的外接圆的圆心位置,并求出圆心坐标;
的外接圆的圆心位置,并求出圆心坐标;
(3)若点 是线段
是线段 下方的抛物线上一点,求
下方的抛物线上一点,求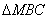 的面积的最大值,并求出此时
的面积的最大值,并求出此时 点的坐标.
点的坐标.

解:(1)将B(4,0)代入抛物线的解析式中,得:
 则
则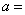

∴抛物线的解析式为:
(2)由(1)的函数解析式可求得:A(﹣1,0)、C(0,﹣2);
∴OA=1,OC=2,OB=4
∴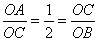 又OC⊥AB,
又OC⊥AB,
∴△OAC∽△OCB
∴∠OCA=∠OBC;
∴∠ACB=∠OCA+∠OCB=∠OBC+∠OCB=90°
∴△ABC为直角三角形,AB为△ABC外接圆的直径
所以该外接圆的圆心为AB的中点,且坐标为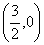
(3)已求得:B(4,0)、C(0,﹣2),可得直线BC的解析式为: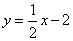
设直线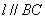 ,则该直线的解析式可表示为:
,则该直线的解析式可表示为: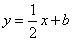 ,当直线
,当直线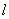 与抛物线只有一个交点时,可列方程:
与抛物线只有一个交点时,可列方程: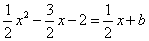 ,且△=0则
,且△=0则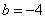
∴直线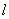 :
: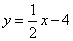 .
.
由于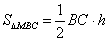 ,
, 长度是定值,则当
长度是定值,则当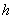 最大(即点M到直线BC的距离最远)时,
最大(即点M到直线BC的距离最远)时,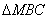 的面积最大
的面积最大
所以点M即直线 和抛物线的唯一交点,则
和抛物线的唯一交点,则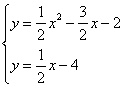
解得: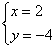
即 M(2,﹣4).


科目:初中数学 来源: 题型:
在整理数据5,5,3,■,2,,4时,■处的数据看不清,但从扇形统计图的答案上发现数据5的圆心角是1800,则■处的数据是( )
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场在“庆五一”促销中推出“1元换2.5倍”活动,小红妈妈买一件标价为600元的衣服,她实际需要付款( )
A.240元 B.280元 C.480元 D.540元
查看答案和解析>>
科目:初中数学 来源: 题型:
在课题学习后,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图3所示,其中,AB表示窗户,且AB=2.82米,△BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线 的最小夹角
的最小夹角 为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中
为18°,最大夹角β为66°,根据以上数据,计算出遮阳蓬中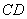 的长是( )
的长是( )
(结果精确到0.1)
(参考数据:sin18°≈0.31,tan18°≈0.32,sin66°≈0.91,tan66°≈2.2)
A.1.2 米 B.1.5米 C.1.9米 D.2.5米
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com