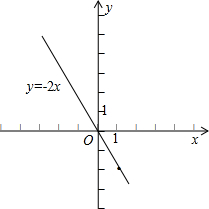(1)解:原式=1+2-5
=-2;
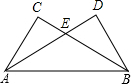
(2)证明:∵在△ACE和△BED中
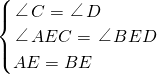
,
∴△ACE≌△BED,
∴AC=BD,CE=ED,
∴AE+ED=BE+CE,
即AD=BC,
∵在△ABC和△BDA中
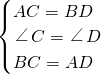
,
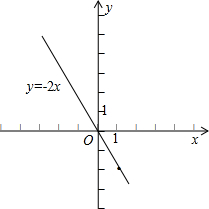
∴△ABC≌△BAD(SAS);
(3)解:当x=1时,y=-2,
即过点(1,-2)和(0,0)作直线即可得出函数y=-2x的图象,如图.
分析:(1)根据幂的乘方、算术平方根、绝对值分别求出每一部分的值,再代入求出即可;
(2)根据AAS证△ACE≌△BED,推出AC=BD,CE=ED,求出AD=BC,再根据SAS证明即可;
(3)在函数上找出两点(1,-2)和(0,0),过此两点作直线即可得出答案.
点评:本题考查了绝对值、幂的乘方、算术平方根、全等三角形的判定和性质、一次函数的图象等知识点,主要考查学生的计算能力和推理能力,全等三角形的判定定理有SAS,ASA,AAS,SSS,一次函数的图象是一条直线.

 (1)计算:
(1)计算: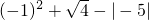 .
.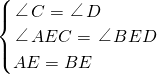 ,
,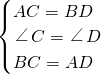 ,
,