
【题目】中国派遣三艘海监船在南海保护中国渔民不受菲律宾的侵犯.在雷达显示图上,标明了三艘海监船的坐标为![]() 、
、![]() 、
、![]() ,(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为
,(单位:海里)三艘海监船安装有相同的探测雷达,雷达的有效探测范围是半径为![]() 的圆形区域(只考虑在海平面上的探测).
的圆形区域(只考虑在海平面上的探测).
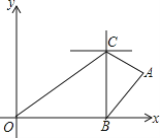
(1)若在三艘海监船组成的![]() 区域内没有探测盲点,则雷达的有效探测半径
区域内没有探测盲点,则雷达的有效探测半径![]() 至少为________海里;
至少为________海里;
(2)某时刻海面上出现一艘菲律宾海警船![]() ,在海监船
,在海监船![]() 测得点
测得点![]() 位于南偏东
位于南偏东![]() 方向上,同时在海监船
方向上,同时在海监船![]() 测得
测得![]() 位于北偏东
位于北偏东![]() 方向上,海警船
方向上,海警船![]() 正以每小时
正以每小时![]() 海里的速度向正西方向移动,我海监船
海里的速度向正西方向移动,我海监船![]() 立刻向北偏东
立刻向北偏东![]() 方向运动进行拦截,问我海监船
方向运动进行拦截,问我海监船![]() 至少以多少速度才能在此方向上拦截到菲律宾海警船
至少以多少速度才能在此方向上拦截到菲律宾海警船![]() ?
?
【答案】(1)50;(2)![]() 海里/小时.
海里/小时.
【解析】
试题(1)利用点的坐标性质得出CO的长,进而利用直角三角形外心的性质得出答案;
(2)利用方向角画出图形,进而利用锐角三角角函数关系得出即可.
试题解析:(1)∵O(0,0)、B(80,0)、C(80,60),
∴BO=80,BC=60,且∠OBC=90°,
∴CO=![]() ,
,
当雷达在CO的中点位置时,正好位于△BCO外心的位置,
此时在三艘海监船组成的△OBC区域内没有探测盲点,雷达的有效探测半径r至少为![]() CO=50(海里);
CO=50(海里);
(2)过点A作AD⊥BC于点D,

设BD=x,由题意得:AD=BD=x,
则tan60°=![]() ,
,
∴CD=![]() ,
,
∴x+![]() =60,
=60,
解得:x=90-30![]() ,
,
设船和舰在点E处相遇,海监船的速度为v海里/小时,过点E作EF⊥AB于点F,设AF=y,由题意得:
AE=![]() y,BE=2y,
y,BE=2y,
∴![]() ,
,
解得:v=20![]() ,
,
答:我海监船B至少以20![]() 海里/小时速度才能在此方向上拦截到菲律宾海警船A.
海里/小时速度才能在此方向上拦截到菲律宾海警船A.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
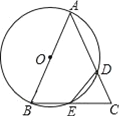
【题目】如图,已知△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于D、E两点,连接ED
(1)求证:△CDE为等腰三角形;
(2)若CD=3,BC=4![]() ,求AD的长和⊙O的半径.
,求AD的长和⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知点A、B是反比例函数y=﹣![]() 上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.
上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题再现:
数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观, 从而可以帮助我们快速解题,初中数学里的一些代数公式,很多都可以通过表示几何图形积的方法进行直 观推导和解释.

![]() 如图 1,是一个重要公式的几何解释,请你写出这个公式:
如图 1,是一个重要公式的几何解释,请你写出这个公式:
![]() 如图 2,在
如图 2,在![]() 中,
中,![]() ,以
,以![]() 的三边长向外作正方形的面积分别为
的三边长向外作正方形的面积分别为![]() ,试猜想
,试猜想![]() 之间存在的等量关系,直接写出结论 .
之间存在的等量关系,直接写出结论 .
![]() 如图 3,如果以
如图 3,如果以![]() 的三边长
的三边长![]() 为直径向外作半圆,那么第
为直径向外作半圆,那么第![]() 问的结论 是否成立?请说明理由.
问的结论 是否成立?请说明理由.
![]() 如图 4,在
如图 4,在![]() 中,
中,![]() ,三边分别为
,三边分别为![]() ,分别以它的三边为直 径向上作半圆,求图 4 中阴影部分的面积.
,分别以它的三边为直 径向上作半圆,求图 4 中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
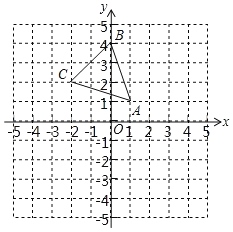
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于y轴对称的△A1B1C1;
(2)点P在x轴上,且点P到点A与点C的距离之和最小,直接写出点P的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,以A(5,1)为圆心,以2个单位长度为半径的⊙A交x轴于点B、C.解答下列问题:
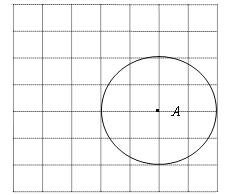
(1)根据A点坐标建立平面直角坐标系;
(2)将⊙A向左平移____________个单位长度与y轴首次相切,得到⊙A,并画出⊙A.此时点A的坐标为_____________.
(3)求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连结BF,CE.下列说法:①△ABD和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com